Comunicación reticente --en los textos de matemáticas
Voy a comentar en este post la tesis de que, si el estudiante va a independizarse tarde o temprano de la escuela y continuar con su aprendizaje de manera autodidacta, lo mejor es que aprenda a leer libros. ("¿Quieres decir que los estudiantes no saben leer? No. Lo que quiero decir es que los libros siguen un cierto estilo de escritura con el cual hay que familiarizarse.") Ilustro la tesis con la redacción clásica de una solución a un problema. Y se empieza a aplicar un método de lectura que ha probado su eficacia en la práctica.
Dos problemas de velocidad
En este post comento dos problemas de velocidad ya en la sección de problemas de MaTeTaM. Le dedico más tiempo al más difícil, tratando de destacar la lógica de su solución. Al final presento un mapa conceptual del razonamiento y la simbolización del difícil, el cual parecería le da más estructura al proceso de resolución.
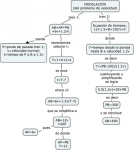
Un problema de velocidades realmente difícil
Un tren de pasajeros parte de la estación A hacia la B a las 13 horas. Después de 6 horas de viaje, el tren se detiene durante 2 horas debido a la acumulación de nieve en la vía. Después de esas 2 horas, el tren prosigue su viaje hacia la estación B, pero ahora con una velocidad 20 porciento mayor que la que mantuvo antes (la velocidad normal). Aún así, llegó a la estación B con una hora de retraso. Al día siguiente, otro tren sale de la estación A hacia la B a las 13 horas y también tuvo que parar durante 2 horas, pero en un punto alejado de A 150 km más que donde paró el primer tren.
Sobre la exención de impuestos en colegiaturas
Me han preguntado varias veces en los últimos días sobre mi opinión acerca del decreto del presidente Calderón sobre la exención de impuestos en colegiaturas. No he dado ninguna lo suficientemente informada pues no conozco a detalle el decreto, y de hecho no lo voy a leer pues tengo otras prioridades. Pero, además, aún cuando lo estudiara y pudiera dar una opinión informada, mi papel de opinador sería percibido por los demás como el de uno más dentro del numeroso grupo de opinadores.
Lo que he opinado es que me parece, en principio, una buena decisión del presidente. Y he tenido que aclarar en qué sentido es buena. Los criterios en que me baso son los siguientes:
Problemas razonados de álgebra... sin álgebra
El problema de edades del post de las 11 preguntas de ENLACE se puede responder sin álgebra, es decir, sin manipulacones algebraicas. Este hecho me llevó a redactar el presente post, el cual puede ser de alguna utilidad para los adolescentes interesados en las matemáticas. El post presenta varios problemas razonados clásicos. Las soluciones aquí presentadas representan una curiosidad de razonamiento lógico, basado en inferencias a partir de los datos y manteniendo la simbolización a un mínimo.
ENLACE Bachillerato: Once problemas tipo
Juego de evocaciones (en un problema de ENLACE bachillerato)
Si bien en la escuela mexicana no es necesaria la eficacia en el problem solving, ésta sí es relativamente importante en los exámenes estandarizados que miden actualmente el desempeño escolar de los adolescentes en matemáticas. Por ejemplo el examen ENLACE --Evaluación Nacional del Logro Académico en Centros Escolares. (ENLACE es importante pues se trata de una mirada externa al quehacer de la escuela y, con un poquito de vergüenza, es muy difícil ignorar su importancia.)
ENLACE 2011 se acerca (prepárate desde hoy)
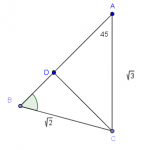
En este post se discuten cuatro problemas de geometría analítica de ENLACE 2010 y se recomiendan algunas estrategias de resolución que han probado su eficacia en la práctica.
ENLACE bachillerato (vive la experiencia on line)
En estos días me puse a resolver el examen en línea ENLACE Bachillerato 2010 y puedo decirles que no está de "enchílame otra". Para empezar les diré que es excesivamente largo: me tomó todo un día resolverlo (dentro de la rutina hogareña de un domingo --es decir, con salidas al centro, visitas, etc.).
