Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Colocación de fichas en el borde de un tablero
Luis tiene un tablero cudriculado con la misma cantidad de filas que de columnas. Las casillas del contorno del tablero están coloreadas de gris. También tiene suficientes fichas numeradas (1,2,3,...) que coloca en las casillas grises de la siguiente manera:
La ficha 1 la pone en la casilla izquierda y, a partir de ahí, el resto las coloca una en cada casilla, consecutivamente de menor a mayor en sentido de las manecillas del reloj. Una vez que llega a la posición inicial sigue colocando fichas sobre las que ya están puestas. Deja de poner fichas cuando observa que los números que están a la vista en las casillas de las esquinas del tablero suman 2012.
Problemas del segundo dia del nacional 12 ONMAS
Números Paceños
Se dice que un número es Paceño si al escribir sus dígitos en orden inverso se obtiene un número mayor que él. Por ejemplo, el 3426 es Paceño porque 6243 es mayor que 3426, mientras que el 774 no es Paceño porque 477 no es mayor que 774. ¿Cuántos números de cinco dígitos son Paceños?
Diferencia de áreas de flores en octágono
A partir de un octágono regular de lado 10 cm, Anita dibuja dos flores como se muestran a continuación:
¿Cuál es la diferencia entre las áreas de las flores?
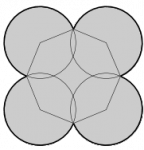
Juego de números en un tablero romboidal
En cada rombo de la figura se coloca un número diferente del 1 al 9. Enseguida, dentro de los círculos se escribe la suma de los dos números que comparten ese lado. Finalmente, se suman los números escritos en los círculos.
De todas las sumas posibles ¿cuál es la diferencia entre la mayor y la menor?

Tesoro de Hernán Cortés --en 2012 cofres
En la Bahía de la Paz, Hernán Cortés guardó su tesoro en 2012 cofres con sus respectivos candados. Cada candado y su cofre están numerados del 1 al 2012. Cortés metió al azar una llave en cada cofre y cerró los candados para que nadie tomara el tesoro. Mucho tiempo después, se halló el tesoro de Cortés. Los arqueólogos van a forzar los candados marcados con los números 1 y 2 para obtener así dos de las llaves con la esperanza de que con ellas sea posible abrir sucesivamente todos los demás cofres. ¿De cuántas maneras pudieron quedar distribuidas inicialmente las llaves dentro de los cofres de manera que la estrategia de los arqueólogos sea exitosa?
Encontrar ángulo dada una bisectriz
En un rectángulo $ABCD$, $F$ es el punto medio del lado $CD$ y $E$ es un punto del lado $BC$ tal que $AF$ es bisectriz del ángulo $EAD$. Si el ángulo $AEF$ mide 68 grados ¿cuál es la medida del ángulo $BAE$?
Múltiplo de cada uno de sus dígitos
Encuentra el mayor número $N$ que cumpla, al mismo tiempo, las siguientes condiciones:
- a) Todos los dígitos de $N$ son distintos,
- b) $N$ es múltiplo de cada uno de sus dígitos.
Los problemas del nacional de la 12 ONMAS
Cuadrados
Hallar el mínimo k>2 para el cual existen k numeros enteros consecutivos tales que la suma de sus cuadrados es un cuadrado
Imposibilidad de nueve rectángulos
Una cuadrícula de $6\times6$ se va a recortar en rectángulos siguiendo las líneas de la cuadrícula. Muestra que no es posible hacer una división de la cuadrícula en 9 rectángulos diferentes.
Área de pentágono
Por los vértices D y A del cuadrado ABCD de lado 5 se trazan, respectivamente, los segmentos paralelos DE y AF hacia afuera del cuadrado, de tal manera DE mide 4 y es perpendicular a EF. Encuentra el área del pentágono ABCEF.
Ecuación de suma de fracciones
Razonado con suma de dígitos
Mauricio ya cumplió años en el 2010. Al sumar los dígitos de la fecha de su nacimiento se dio cuenta que obtenía su edad. ¿Cuántos años puede tener Mauricio?
Seccionado de un cubo de lado $3$
Un cubo de lado 3 se divide en 27 cubitos unitarios. ¿De cuántas formas podemos elegir tres cubitos de manera que sus centros estén en una misma recta? Nota: El centro de un cubito se localiza en el punto medio de una diagonal mayor.
Demostrar perpendicular
Sean $ABC$ un triángulo rectángulo y $M$ el punto medio de la hipotenusa $BC$. Sus catetos cumplen que $CA$ es menor que $AB$. Se coloca un punto $D$ sobre $AB$ de manera que $CA = AD$. Finalmente, sea $E$ el punto común de $AM$ y $CD$. Si $F$ es un punto sobre $BC$ tal que $EF$ es paralela a BC $AC$, demostrar que $AM$ es perpendicular a $FD$.
Tangentes a circunferencia desde el centro de otra
Considere las circunferencias $a$ y $b$ de centros $A$ y $B$ respectivamente. Desde el centro $A$ se trazan las tangentes a $b$ y éstas cortan a $a$ en los puntos $P$ y $Q$. Desde el centro $B$ se trazan las tangentes a $a$ que cortan a $b$ en $R$ y $S$. Demostrar que $PQRS$ es un rectángulo.
Número igual a la suma del factorial de sus dígitos
Encontrar todos los números de 3 dígitos de la forma $abc$ ($a$ es el dígito de las centenas, $b$ es el dígito de las decenas y $c$ es el dígito de las unidades) que cumplan con: $abc = a!+b!+c!.$ (Nota: n! es el producto n(n-1)...(2)(1) y se lee $n$ factorial.)
Sumas de productos de filas y columnas en un tablero
En un tablero de 2009 x 2009 cuadritos, se han llenado todos los cuadritos usando solamente 1 o -1, y se ha obtenido el producto de los números de cada fila y de cada columna. Encontrar todas las posibles sumas de estos 4018 productos.
Ejemplo: en un tablero de 3x3 un posible llenado es:
1 1 1
1 1 -1
1 1 1
y la suma de los 6 productos 1 + 1 -1 +1 -1 +1 = 2
Elección condicionada de 3
¿De cuántas maneras se pueden escoger 3 números diferentes del conjunto $C=\{1,2,3,...,19,20\}$ de manera que la suma de esos tres números sea múltiplo de 3?
