Problemas
También puedes compartirnos alguno de tus problemas favoritos:
El odómetro chafa
El odómetro (medidor de distancias recorridas) de un carro chafa siempre brinca de 3 a 5, saltándose el 4, sin importar la posición. Por ejemplo, después de viajar un kilómetro cambió de 000039 a 000050. Si el odómetro marca 002005, ¿cuántos kilómetros ha viajado en realidad el carro chafa?
Fichas en progresión aritmética
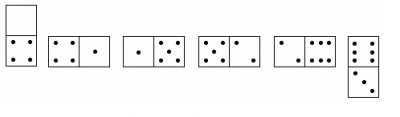
Como se ve en la ilustración se han jugado seis fichas de dominó. De acuerdo a las reglas del juego, se une 4 con 4, 1 con 1, y así sucesivamente. Para el caso de la figura, la suma de los puntos de cada ficha son 4, 5, 6, 7, 8, 9 y están en progresión aritmética, es decir, los números tomados en orden tienen una diferencia común, en este caso particular el 1.
¿De cuántos modos podemos jugar seis fichas de dominó, tomadas de una caja común de veintiocho, para que los números queden en progresión aritmética?
Años superolímpicos
Cuando la edición N de la ONMAS se realiza en un año divisible entre N, diremos que es un año superolímpico. Por ejemplo el año 2005 es superolímpico porque se realiza la edición 5 de la ONMAS y 2005 es divisible entre 5. Determina todos los años superolímpicos, sabiendo que la ONMAS se realiza anualmente a partir de 2001 y suponiendo que se seguirá realizando cada año.
Triángulos en una circunferencia
Sean AB es el diámetro de una circunferencia con centro en el punto D, y C un punto en AB de tal manera que AC es la mitad de CB. Por el punto C se traza una perpendicular a AB que corta a la circunferencia en los puntos E y F. Si el área del triángulo ABE es de 60cm2 ¿cuánto vale el área del triángulo DEF?
EGMO Problema 2 - Máxima cantidad de renglones en una tabla
Sea n un entero positivo, encuentra el entero más grande m, en términos de n con la siguiente propiedad:
Una tabla con m renglones y n columnas puede ser llenada con números reales de tal manera que dos diferentes renglones, [a1,a2,…,an] and [b1,b2,…,bn] satisfacen que max(|a1−b1|,|a2−b2|,…,|an−bn|)=1.
©Traducido de la versión en ingles por Matetam.com
EGMO Problema 1 - Sobre dos circuncentros y demostrar que una línea es perpendicular
Sea ABC un triángulo con circuncentro O. Los puntos D, E y F se encuntran en el interio de los lados BC, CA y AB respectivamente, de tal manera que DE es perpendicular a CO y DF such that DE is perpendicular to CO and DF is perpendicular to BO. (Por punto interior nos referimos, por ejemplo, a que el punto D se encuentra sobre la línea BC y D está entre B y C en esa línea)
Consideremos K el circuncentro del triángulo AFE. Desmuestra que las líneas DK y BC son perpendiculares.
©Traducido de la versión en ingles para Matetam.com
Numeros aluxes
Un entero positivo n es aluxe si el producto de los digitos de n es igual al producto de los digitos de n+1. ¿Cuántos enteros aluxes hay menores o iguales a 2011 y mayores o iguales a 1?
Juego de intercambios con piedras coloreadas
Sean k y n enteros positivos con k≥2. En una línea recta se tienen kn piedras de k colores diferentes. de tal forma que hay n piedras de cada color. Un paso consiste en intercambiar de posición dos piedras adyacentes. Encontrar el menor entero positivo m tal que siempre es posible lograr con a lo sumo m pasos que las n piedras de cada color queden seguidas si:
- a) n es par,
- b) n es impar y k=3
Desigualdad con multiplicadores en {−1,1}
Sean x1,x2,…,xn números reales positivos. Demostrar que existen a1,a2,…,an∈{−1,1} tales que a1x21+a2x22+…+anx2n≥(a1x1+a2x2+…+anxn)2
Ortocentro de un acutángulo
Sea ABC un triángulo acutángulo con AC≠BC, y sea O su circuncentro. Sean P y Q puntos tales que BOAP y COPQ son paralelogramos. Demostrar que Q es ortocentro de ABC.
Triángulo con incírculo y tres circunferencias más
Sea ABC un triángulo y sean X,Y,Z los puntos de tangencia de su incírculo con los lados BC,CA,AB, respectivamente. Suponga que C1,C2,C3 son circunferencias con cuerdas XY,ZX,YZ, respectivamente, tales que C1 y C2 se cortan sobre la recta CZ y que C1 y C3 se corten sobre la recta BY. Suponga que C1 corta a las cuerdas XY y ZX en J y M, respectivamente; que C2 corta a las cuerdas YZ y XY en L e I, respectivamente; y que C3 corta a las cuerdas YZ y ZX en K y N, respectivamente. Demostrar que I,J,K,L,M,N están sobre una misma circunferencia.
Ecuación de inversos OIM 2011
Encontrar todos los enteros positivos n para los cuales existen tres enteros no nulos x,y,z tales que x+y+z=0 y 1x+1y+1z=1n
Por 2, por 3 o más uno
En la pizarra está escrito el número 2. Ana y Bruno juegan alternadamente, comenzando por Ana. Cada uno en su turno sustituye el número escrito por el que se obtiene de aplicar exactamente una de las siguiente operaciones: multiplicarlo por 2 o multiplicarlo por 3 o sumarle 1. El primero que obtenga un resultado mayor o igual a 2011 gana. Decidir quién tiene una estrategia ganadora y describirla.
Mesa redonda con vasijas y personas
Alrededor de una mesa redonda hay 12 personas, y sobre la mesa hay 28 vasijas. Una persona puede ver a otra si y sólo si no hay ninguna vasija alineada con ellos. Demostrar que hay por lo menos dos personas que se pueden ver la una a la otra.
Colinealidad en configuración de cíclico con ortodiagonales
Sea ABCD un cuadrilátero cíclico cuyas diagonales AC y BD son perpendiculares. Sean O el circuncentro de ABC, K el punto de intersección de las diagonales, L≠O el punto de intersección de las circunferencias circunscritas a OAC y OBD, y G el punto de intersección de las diagonales del cuadrilátero cuyos vértices son los puntos medios de los lados de ABCD. Demostrar que O,K,L,G están alineados.
Medias enteras
Las medias aritmética, geométrica y armónica de dos enteros positivos distintos son todas números enteros. Hallar el menor valor posible de la media aritmética de los dos enteros.
Concurrencia en configuración de in y circuncírculos
Sea Γ el incírculo de un triángulo escaleno ABC, que es tangente a los lados BC,CA,AB en los puntos D,E,F respectivamente. Las rectas EF y BC se cortan en G. La circunferencia de diámetro GD corta a Γ por segunda vez en R. Sean P y Q los puntos de intersección (distintos de R) de Γ con BR y CR, respectivamente. Las rectas BQ y CP se cortan en X, el circuncírculo de CDE corta a QR en M y el circuncírculo de BDF corta a PR en N. Demostrar que PM,QN y RX son concurrentes.
Sucesión en enteros indecisa
Decidir si existen enteros positivos a y b tales que todos los términos de la sucesión (Xn), definida como X1=2010,X2=2011, Xn+2=Xn+Xn+1+a√XnXn+1+b son números enteros.
Diez monedas, dos preguntas
Se tienen diez monedas indistinguibles en hilera. Se sabe que dos de ellas son falsas y están en posiciones consecutivas en la hilera. Una pregunta consiste en elegir un subconjunto cualquiera de las monedas y preguntar cuántas de ellas son falsas. Decidir si es posible identificar con certeza las monedas falsas haciendo solamente dos preguntas, sin conocer la respuesta de la primera antes de formular la segunda.
Números racionales!!!
Demuestra que la suma de las raíces cuadradas de 2 y 3 suman un número irracional. Esto es, √2+√3 es irracional.
