Problemas - Combinatoria
P3 IMO 1993 - Tablero de ajedrez infinito
Sobre un tablero de ajedrez infinito se juega de la siguiente manera:
Al principio hay $n^2$ fichas dispuestas sobre el tablero en un cuadrado de $n\times n$ de casillas adyacentes, con una ficha en cada casilla. Cada jugada es un salto de una ficha en dirección horizontal o vertical sobre una casilla adyacente, ocupada por otra, hasta una no ocupada, contigua a ella. La ficha sobre la que se ha saltado se retira. Halle los valores de $n$ para los que el juego puede terminar quedando una única ficha en el tablero.
Secuencia de conjuntos no vacios (OMM 2021 P6)
Determina todos los conjuntos no vacíos $C_1, C_2, C_3, \dots$, tales que cada uno de ellos tiene un número finito de elementos y todos sus elementos son enteros positivos, con la siguiente propiedad: Para cualesquiera enteros positivos $m$ y $n$, la cantidad de enteros positivos en el conjunto $C_m$ más la cantidad de enteros positivos en $C_n$ es igual a la suma de los elementos en el conjunto $C_{m+n}$.
Nota: Al denotar con $|C_k|$ la cantidad de elementos de $C_k$ y con $S_k$ la suma de los elementos de $C_k$, la condición del problema es que para $m$ , $n$ enteros positivos se cumple
$$|C_n|+|C_m| = S_{m+n}$$La hormiga, el mago y la lava (OMM 2021 P3)
Sean $m,n \geq 2$ dos enteros. En una cuadrícula de $m \times n$, una hormiga empieza en cuadrito inferior izquierdo y quiere camina al cuadradito superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, de acuerdo a las siguientes posibilidades $\uparrow$, $\rightarrow$ y $\nearrow$. Sin embargo, un malvado mago ha dejado caer lava desde arriba y ha destruido algunos cuadritos de forma tal que:
Pasa los caballos a las columnas, si puedes...
En un tablero de ajedrez de $2017 \times 2017$, se han colocado en la primera columna 2017 caballos, uno en cada casilla de la columna. Una tirada consiste en elegir dos caballos distintos y de manera simultánea moverlos como se mueven los caballos de ajedrez. Encuentra todos los posibles valores enteros de $k$ con $1\leq k \leq 2017$, para los cuales es posible llegar a través de varias tiradas, a que todos los caballos estén en la columna $k$, uno en cada casilla.
Nota. Un caballo se mueve de una casilla $X$ a una $Y$, solamente si $X$ y $Y$ son las esquinas opuestas de un rectángulo de $3\times 2$ o de $2 \times 3$.
Problema clásico con solución atípica
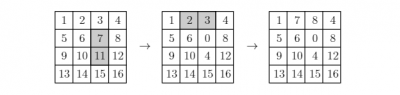
En una cuadrícula de $ n \times n$ se escriben los números del 1 al $n^2$ en orden, por renglones, de manera que en el primer renglón aparecen los números del 1 al n, en el segundo los números del n+1 al 2n, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen esos dos cuadraditos. Por ejemplo, aquí abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de 4x4: primero restando 7 a los cuadraditos sombreados y luego sumando 5 a los sombreados.
Múltiplo de 7 con dígitos consecutivos
Decimos que un número entero no-negativo $n$ contiene a otro número entero no-negativo $m$, si los dígitos de su expansión (o desarrollo) decimal aparecen en forma consecutiva en la expansión (o desarrollo) decimal de $n$. Por ejemplo 2016 contiene a 2,0,1,6, 20, 16, 201 y 2016. Determina el mayor número entero $n$ que no contiene a ningún múltiplo de 7.
Parejas Guerreras
Una pareja de enteros positivos $m,n$ es guerrera si existen enteros positivos $a,b,c,d$ con $m=ab, n=cd$ y $a+b=c+d$. Por ejemplo, la pareja 8,9 es guerrera pues $8 = 4 \cdot 2 , 9=3 \cdot 3$ y $4+2=3+3$. Se colorean los enteros positivos de la siguiente manera:
- Empezamos coloreando el 3 y el 5.
- Después , si algún entero positivo no está coloreado y este tiene una pareja guerrera que ya está coloreado, entonces lo coloreamos.
Encuentra todos los enteros positivos que eventualmente se colorean.
Cuadritos unitarios distanciados
Considera un tablero de $n \times n$, con $n \geq 5$. Dos cuadritos unitarios se dice que son distanciados si no se encuentran en el mismo renglón ni en renglones consecutivos y tampoco en la misma columna ni en columnas consecutivas. Se toman 3 rectángulos con vértices y lados sobre los puntos y lineas del tablero de manera que si dos cuadritos unitarios pertencen a distintos rectángulos entonces son distanciados . ¿De cuántas maneras es posible hacer esto?
Triángulos Tranquilos
Considera un tablero cuadrículado de manera regular cuya área es $N$. Al colocar un triángulo no degenerado dentro de él (que puede quedar en los bordes) decimos que es tranquilo, si cada vértice coincide con algún vértice de los cuadritos unitarios interiores, además si uno de sus lados es paralelo a algún lado del tablero. Supón que se han colocado $N+1$ triángulos tranquilos, muestra que hay dos con la misma área.
Problema 2 - IMO 2016 - Las letras de IMO en un tablero
Hallar todos los enteros positivos $n$ para los que en cada casilla de un tablero de $n \times n$ puede escribir una de las letras $I$, $M$ y $O$ de manera que: