Publicaciones Recientes
P4 OMM 2002. Hileras de dominó --con suma impar
Una ficha de dominó tiene dos números (no necesariamente diferentes) entre 0 y 6. Las fichas se pueden voltear, es decir, $[4,5]$ es la misma ficha que $[5,4]$. Se quiere formar una hilera de fichas de dominó distintas, de manera que, en cada momento de la construcción de la hilera, la suma de todos los números de las fichas puestas hasta ese momento sea impar. Las fichas se pueden agregar de la manera usual a ambos extremos de la hilera, es decir, de manera que en cualesquiera dos fichas consecutivas aparezca el mismo número en los extremos que se juntan.
P3 OMM 2002. Residuos cuadráticos (módulo 4)
Sean $n$ un entero positivo. ¿Tiene $n^2$ más divisores positivos de la forma $4k+1$ o de la forma $4k-1$?
P2 OMM 2002. Circuncírculo de la mitad de un paralelogramo
Sean $ABCD$ un paralelogramo y $\kappa$ la circunferencia circunscrita al triángulo $ABD$. Sean $E$ y $F$ las intersecciones de $\kappa$ con los lados (o sus prolongaciones) $BC$ y $CD$, respectivamente ($E$ distinto de $B$ y $F$ distinto de $D$). Demuestra que el circuncentro del triángulo $CEF$ está sobre $\kappa$.
P1 OMM 2002. Operaciones sobre cuadrícula 32X32
En una cuadrícula de $32\times32$ se escriben los números del 1 al 1024 de izquierda a derecha: los números del 1 al 32 en el primer renglón, los del 33 al 64 en el segundo, etc. La cuadrícula se divide en cuatro cuadrículas de $16\times16$ que se cambian de lugar entre ellas como sigue:
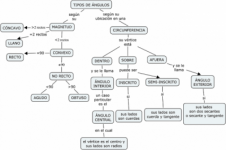
Clasificación de ángulos
Parecería que de ángulos hay muy poco que decir. Son los objetos geométricos que se miden con un transportador ¿cierto? Cierto, pero hay toda una terminología escolar que el aprendiz debería aprender.
En lo que sigue voy a hablar primero de una clasificación de los ángulos, y en la segunda parte voy plantear la clasificación de las relaciones entre dos ángulos. En cada una de esas clasificaciones se presenta primero un mapa conceptual y después se hace el mismo planteamiento pero de manera discursiva.
Problema 6, IMO 2010
Sea $a_1, a_2, a_3, \ldots$ una sucesión de números reales positivos. Se tiene que para algún entero positivo $s$,
$$a_n = \textrm{max}\{a_k + a_{n-k} \textrm{ tal que } 1 \leq k \leq n - 1\}$$
para todo $n > s$. Demuestre que existen enteros positivos $\ell$ y $N$, con $\ell \leq s$, tales que $a_n = a_\ell + a_{n-\ell}$ para todo $n \geq N$.
Problema 3, IMO 2010
Sea $\mathbb{N}$ el conjunto de los enteros positivos. Determine todas las funciones $g : \mathbb{N} \to \mathbb{N}$ tales que $$\left( g(m) + n\right) \left(m + g(n) \right) $$
es un cuadrado perfecto para todo $m, n \in \mathbb{N}$.
Problema 5, IMO 2010
En cada una de las seis cajas $B_1,B_2,B_3,B_4,B_5,B_6$ hay inicialmente sólo una moneda. Se permiten dos tipos de operaciones:
- Tipo 1: Elegir una caja no vacía $B_j$ , con $1 \leq j \leq 5$. Retirar una moneda de $B_j$ y añadir dos monedas a $B_{j+1}$.
- Tipo 2: Elegir una caja no vacía $B_k$, con $1 \leq k \leq 4$. Retirar una moneda de $B_k$ e intercambiar los contenidos de las cajas (posiblemente vacías) $B_{k+1}$ y $B_{k+2}$.
Determine si existe una sucesión finita de estas operaciones que deja a las cajas $B_1,B_2,B_3,B_4,B_5$ vacías y a la caja $B_6$ con exactamente $2010^{2010^{2010}}$ monedas. (Observe que $a^{b^c} = a^{(b^c)}$.)
Problema 2, IMO 2010
Sea $ABC$ un triángulo, $I$ su incentro y $\Gamma$ su circunferencia circunscrita. La recta $AI$ corta de nuevo a $\Gamma$ en $D$. Sean $E$ un punto en el arco $\widehat{BDC}$ y $F$ un punto en el lado $BC$ tales que
$$\angle BAF = \angle CAE < \frac{1}{2} \angle BAC.$$
Sea $G$ el punto medio del segmento $IF$. Demuestre que las rectas $DG$ y $EI$ se cortan sobre $\Gamma$.
Problema 4, IMO 2010
Sea $P$ un punto en el interior del triángulo $ABC$ con circunferencia circunscrita $\Gamma$. Las rectas $AP,BP,CP$ cortan otra vez a $\Gamma$ en los puntos $K,L,M$, respectivamente. La recta tangente a $\Gamma$ en $C$ corta a la recta $AB$ en $S$. Demostrar que si $SC=SP$ entonces $MK=ML$.
