Publicaciones Recientes
Problemas de un examen estatal de OMM Jalisco
Sucesiones, recursividad y diferencias finitas
En este post voy a abordar de nuevo el tema de la recursividad a través de algunas sucesiones definidas de manera recursiva. Puesto que la recursión es un tipo de razonamiento muy útil en el problem solving de combinatoria, voy a plantear primero algunos ejemplos de modelación, un tema que se omite en la mayoría de los textos sobre el tema.

Competencia entre 7 jugadores!!!
Se quiere diseñar una competencia entre 7 jugadores de tal manera que de cualquier colección de 3 de ellos al menos dos compitan entre sí. ¿Cuál es el mínimo número de juegos con el que se puede lograr esta condición?
Triángulos semejantes
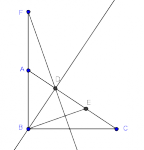
Sea XYZ un triángulo rectángulo con <Z=90°. Prolonguemos el lado XZ y marcamos un punto A tal que XZ=ZA y Z queda entre X y A. Prolongar el lado YZ y marcamos un punto B tal que YZ=ZB y Z queda entre Y y B. Trazamos la altura ZW (W en XY) del triángulo XYZ y prolongamos hasta un punto C tal que ZW=WC, y W queda entre Z y C. Si el área de XYZ es 30. Encuentra el valor del area del triángulo ABC
Una muy fácil de álgebra!!!
En un evento académico de la SEG (SECRETARIA DE EDUCACION GUERRERO) se planteó el siguiente problema:
Una taza de café está a 80° C, al colocarla en un enfriador pierde el 5% de temperatura por segundo, construye el modelo algebraico de esta situación con la argumentación adecuada.
EGMO Problema 4 - Conjunto de enteros llenos por sumas y libres de sumar cero
Un conjunto A de enteros es llamado lleno por sumas si A⊆A+A, es decir, que cada elemento a∈A es la suma de algún par (no necesarimante distintos) de elementos b,c∈A.
Un conjunto A de enteros es llamado libre de sumar cero si 0 es el único entero que no puede ser expreado como la suma de los elementos de un subconjunto finito y no vacio de A.
¿Existirá un conjunto de enteros lleno por sumas y libre de sumar cero?
Testamento..... A ver si puedes
La mamá de Vero esta haciendo su testamento. A sus tres hijas le dará en herencia el número de pesos que calculen como sigue:
EGMO 2012 Problema 3 - Relación funcional en los reales
Entontrar todas las funciones f:R→R tales que: f(yf(x+y)+f(x))=4x+2yf(x+y) para todo x,y∈R.
©Traducido de la versión en ingles para Matetam.com
El misterioso hechizo del problem solving
En días pasados subí a MaTeTaM todos los problemas de la ONMAS que pude encontrar, y hubo uno que ya había publicado en 2010 y que llamó mi atención pues se ve bastante difícil... y más difícil es la solución que envió Brandon en su momento (basada en una semejanza).
Bueno, lo difícil es entender la demostración que da de la semejanza --yo no le entendí. El caso es que lo traje en al cabeza varios días, lo resolví de otra manera (por ortocentro) y generé un problema parecido... pero no podía demostrar la semejanza (que parecía obvia en la figura) de una manera alternativa a la que dio Brandon.
Perímetro de hexágono --con dos equiláteros superpuestos
Dos triángulos equiláteros ABC y DEF de perímetros 36 y 27 centímetros, respectivamente, están sobrepuestos, formando un ángulo de 120 grados como se muestra en la figura. Calcula el perímetro del hexágono sombreado.
