Geometría

Con centro en el incentro I, de un triángulo ABC se traza una circunferencia que corta en dos puntos a cada uno de los tres lados del triángulo: al segmento BC en D y P (siendo D el más cercano a B); al segmento CA en E y Q (siendo E el más cercano a C), y al segmento AB en F y R (siendo F el más cercano a A).

Sea S el punto de intersección de las diagonales del cuadrilátero EQFR. Sea T el punto de intersección de las diagonales del cuadrilátero FRDP. Sea U el punto de intersección de las diagonales del cuadrilátero DPEQ.

Sean $n \geq 2$ un número entero y $D_n$ el conjunto de puntos $(x,y)$ del plano cuyas coordenadas son números enteros con $-n \leq x  \leq n$ y $-n \leq y \leq n$

 Demuestra que, para un triángulo no equilátero, el circuncentro, el gravicentro y el ortocentro están sobre una misma recta.

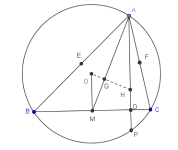
 En la figura se muestra un triángulo $ABC$ y su circuncírculo. El segmento que va desde el circuncentro $O$ (concurrencia de mediatrices) al gravicentro $G$ (concurrencia de medianas) se ha prolongado hasta cortar a la altura $AD$ en $H$.

Demostrar:

• (a) Los triángulos $OMG$ y $HAG$ son semejantes
• (b) El segmento $GH$ mide el doble que el $OG$
• (c) En $H$ concurren las tres alturas

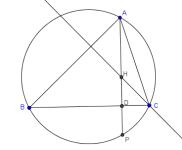
En la figura, $H$ es la intersección de las alturas, y la altura $AD$ del triángulo $ABC$ se ha prolongado hasta cortar el circuncírculo en $P$.

Demostrar:

• (a) El triángulo $HBC$ es isósceles
• (b) La recta $BC$ es mediatriz de $HP$
• (c) Los puntos $H$ y $P$ son simétricos respecto al lado $BC$

 Demostrar que, en cualquier triángulo, el punto simétrico del ortocentro respecto a un lado es un punto del circuncírculo.

Sean $C_1$ y $C_2$ dos circunferencias tangentes exteriormente en un punto $A$. Se traza una recta tangente a $C_1$ en $B$ y secante a $C_2$ en $C$ y $D$; luego se prolonga el segmento $AB$ hasta intersecar a $C_2$ en un punto $E$. Sea $F$ el punto medio del arco $CD$ sobre $C_2$ que no contiene a $E$ y sea $H$ la intersección de $BF$ con $C_2$. Muestra que $CD,AF$ y $EH$ son concurrentes.

 En el triángulo acutángulo $ABC$, los puntos $D,E,F$, ubicados respectivamente en los lados $BC,CA,AB$, son tales que $$CD/CE=CA/CB$$ $$AE/AF=AB/AC$$ $$BF/BD=BC/BA$$ Demostrar que $AD,BE,CF$ son alturas.

 En el triángulo $ABC$, el ángulo $BAC$ mide 60 grados. La bisectriz del ángulo $ABC$ corta al lado $AC$ en $X$ y la bisectriz del ángulo $BCA$ corta  al lado $AB$ en $Y$. Demuestra que si $I$ es el incentro del triángulo $ABC$, entonces $IX=IY$