Avanzado

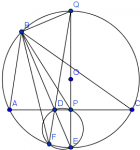
Considera un triangulo $ABC$ Con $BD$ su bisectriz interna ( $D$ sobre $AC$) Sea $E$ el punto donde se intersectan $BD$ y el circuncirculo del triangulo $ABC$. El circulo de diametro $DE$ corta al circuncirculo del triangulo $ABC$ en los puntos $D,F$ demuestra que $BF$ es la simediana del triangulo $ABC$

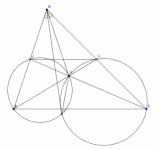
Sea $MN$ una línea paralela al lado $BC$ del triángulo $ABC$, con $M$ sobre el lado $AB$ y $N$ sobre el lado $AC$. Las íineas $BN$ y $CM$ se intersectan en un punto $P$. Los circuncírculos de los triángulos $BPM$ y $CPN$ se intersectan en $P$ y $Q$. Demostrar que $\angle{BAQ}=\angle{CAP}$

Sean H,O el ortocentro y circuncentro del triangulo ABC con AB distinto de AC. Sea T la circunferencia circunscrita al triangulo ABC. La prolongacion de la mediana AM del triangulo ABC, corta a T en el punto N y la circunferencia de diametro AM corta a T en los puntos A y P. Demuestra que las rectas AP, BC y OH son concurrentes si y solo si AH=NH

Sea $ABC$ un triángulo con incentro $I$ y $AB$  menor que $AC$. Sean $D,E,F$  los puntos de tangencia del incírculo con los lados $BC,CA, AB$, respectivamente. Sean $H$  la intersección de $BI$ con $EF$, y $G$ la intersección de $CI$ con $EF.$ 

a) Demostrar que $I$ es el incentro del triángulo $DGH.$

b) Demostrar que las rectas $BG$ y $CH$ concurren sobre la perpendicular a $BC$ que pasa por $D.$

En un circunferencia hay $3n$ puntos que la dividen en $3n$ arcos. De estos arcos $n$ miden 1,  $n$ miden 2 y el resto mide 3. Demuestra que existen dos de estos puntos diametralmente opuestos.

Sea $P=\{P_1, P_2, \dots, P_{1997}\}$ un conjunto de 1997 puntos en el interior de un círculo de radio 1, siendo $P_1$ el centro del círculo. Para cada $k=1, \dots, 1997$ sea $x_k$ la distancia de $P_k$ al punto de $P$ más próximo a $P_k$ y distinto de $P_k$. Demostrar que:

Dentro de un pentágono de área 1993 se encuentran 995 puntos. Considere estos puntos junto con los vértices del pentágono.

Muestre que, de todos los triángulos que se pueden formar con los 1000 puntos anteriores como vértices, hay al menos uno de área menor o igual que 1.

Encontrar todos los enteros positivos $n$ para los cuales el conjunto $A= \{n, n+1, n+2, n+3, n+4, n+5\}$ puede particionarse en dos subconjuntos con el mismo producto de sus miembros (el producto de los números en uno de los subconjuntos es igual al producto de los números en el otro).
 

Sea $ABC$ un triángulo y sean $D$, $E$ y $F$ los puntos donde la circunferencia circunscrita es tangente al lado $BC$, $CA$ y $AB$. Llamemos $D'$ el punto donde la recta $EF$ corta a la recta $AB$. Demuestra que:

a) $D'$ es el conjugado armónico de $D$ con respecto al segmento $AB$.

b) Que la recta $AD$ es la polar de $D'$ respecto al incírculo.

Demuestra que si $p$ es un primo impar que divide a $n^2 +1$ para algún $n$, entonces $p$ debe ser de la forma $4k+1$, es decir, $p \equiv 1$ (mód  4).