Avanzado

Encontrar las tres últimas cifras de $2009^{9999}$ (argumento fiador requerido).

Demostrar que en un conjunto de 18 números enteros positivos, consecutivos y  menores o iguales a 2009, hay uno que es divisible entre la suma de sus cifras.

Resolver la ecuación diofantina siguiente para enteros no negativos x,y,z:

$$x^2+y^4+z^6=2^{1111}$$

Encontrar todas las tripletas $(p,q,r)$ de números primos tales que $p^q+p^r$ es un cuadrado perfecto.

 Sea n un entero positivo. Consideremos la suma $x_1y_1 + x_2y_2 + \ldots + x_ny_n$, donde los valores que pueden tomar las variables $x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n$ son únicamente 0 y 1. Sea $I(n)$ el número de $2n$-adas $(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n)$ para las cuales el valor de la suma es un número impar y sea $P(n)$ el número de $2n$-adas $(x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n)$ para las cuales la suma toma valor par. Probar que

$$\frac{P(n)}{ I(n)}=\frac{2^n + 1}{2^n - 1}$$

Sea $n$ un entero positivo y sean $a_1,a_2,...,a_k (k\geq 2)$ enteros distintos del conjunto ${1,...,n}$, tales que $n$ divide a $a_i(a_{i+1}-1)$, para $i=1,..., k-1$. Demostrar que $n$ no divide a $a_k(a_1-1)$.

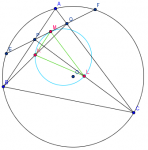
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.

En un triángulo $ABC$, donde $AB=AC$, los bisectrices internas de $\angle{A}$ y $\angle{B}$ cortan a los lados $BC$ y $AC$ en $D$ y $E$, respectivamente. Sea $I$ el incentro del triángulo $ADC$. Supongamos que $\angle{IEB}=45$. Encontrar todos los valores posibles de $\angle{A}$.

Sean $P$ un punto en el interior de una circunferencia $\mathcal{C}$ y $M$ un punto sobre $\mathcal{C}$. Definamos $N$ el punto sobre $\mathcal{C}$ tal que el ángulo $\measuredangle MPN = 90^{\circ}$ (en sentido contrario de las manecillas del reloj). Llamemos $P'$ el punto que resulta de reflejar $P$ con respecto a $MN$.

Sea $ABCD$ un cuadrilatero convexo con $BC=DA$ y además las rectas $BC,DA$ no son paralelas. Consideremos dos puntos variables $E,F$ sobre $BC, DA$ respectivamente, que satisfacen $BE=DF$ . Sea $P$ la interseccion de $AC, BD.$  Las rectas $BD$ y $EF$ se intersectan en $Q$ y las rectas $AC$ y $EF$ se intersectan en $R$.