Como se sabe, la Olimpiada Iberoamericana de Matemáticas se realizó esta semana en Cochabamba.  Enseguida presento los problemas tomados del facebook de la OMM  (de una comunicación de Amanda Rhoton). 

Equiláteros en un rectángulo

A continuación se presentan las soluciones del concurso ciudades con que inició el proceso de selección de la OMM en Tamaulipas 2012 el viernes 21 de septiembre. 

A continuación se presentan los problemas del concurso ciudades con que inició --el viernes 21 de septiembre-- el proceso de selección Tamaulipas 2012 para la XXVI Olimpiada Mexicana de Matemáticas --cuyo concurso nacional se realizará en noviembre en Guanajuato. Se añaden algunos comentarios de parte del que esto escribe --a partir de los enunciados y de las soluciones presentadas por los concursantes...

Los problemas

1G. En el segmento AB se elige un punto E. En los extremos de AB se levantan dos segmentos AD y BC, perpendiculares a AB, de tal manera que AD=AE y BC=BE. Demostrar que el triángulo CDE es rectángulo en E.

Tarde pero sin sueño --como dicen en Viento Libre--, el proceso de selección de la OMM en Tamaulipas inicia en este mes de septiembre. Así que se les notifica (de manera extraoficial) a todos los adolescentes interesados en las matemáticas de Tamaulipas para que se preparen para la etapa municipal. El calendario es el siguiente:

En los problemas de la IMO, la dificultad para un aficionado a las matemáticas de concurso (como el que esto escribe) no es el resolverlos (esa es casi una imposibilidad) sino el entender las soluciones publicadas. Voy a comentar en este post las soluciones de los problemas 1 y 5 de la 53 International Mathematical Olympiad (2012) que se celebró en Mar del Plata (Argentina) del 4 al 16 de julio.

Para el problema 1 me faltaba un teorema, para el 5 el plan de solución. Es decir, para el 5 la solución publicada la podía seguir, pero me quedaba la incógnita de por qué o cómo esa ruta de solución era la correcta o por qué. 

Felicidades para la delegación mexicana. Y obviamente para Diego.

Los saluda

jmd

4. Hallar todas las funciones $f:Z\rightarrow Z$ que cumplen la siguiente igualdad:

$$f(a)^2+f(b)^2+f(c)^2=2f(a)f(b)+2f(b)f(c)+2f(c)f(a).$$
para todos los enteros $a,b,c$ que satisfacen $a+b+c=0$
($Z$ denota el conjunto de los números enteros.)

5. Sea $ABC$ un triángulo tal que $\angle{BCA}=90$, y sea $D$ el pie de la altura desde $C$. Sea $X$ un punto interior del segmento $CD$. Sea $K$ el punto del segmento $AX$ tal que $BK=BC$. Análogamente, sea $L$ el punto del segmento $BX$ tal que $AL=AC$. Sea $M$ el punto de intersección de $AL$ y $BK$. Demostrar que $MK=ML$

6. Hallar todos los enteros positivos $n$ para los cuales existen enteros no negativos $a_1,a_2\ldots,a_n$ tales que

1. Dado el triángulo $ABC$, el punto $J$ es el centro del excírculo opuesto al vértice $A$. Este excírculo es tangente al lado $BC$ en $M$, y a las rectas $AB$ y $AC$ en $K$ y $L$, respectivamente. Las rectas $LM$ y $BJ$ se intersecan en $F$, y las rectas $KM$ y $CJ$ se intersecan en $G$. Sea $S$ el punto de intersección de las rectas $AF$ y $BC$. Demostrar que $M$ es el punto medio de $ST$.

2. Si los reales positivos $a_2,a_3,\ldots, a_n$ satisfacen $a_2\cdot a_3 \cdots a_n=1$, demostrar que
$$(a_2+1)^2(a_3+1)^3\cdots(a_n+1)^n \gt n^n$$

3. El juego de la adivinanza del mentiroso es un juego para dos jugadores $A,B$. Las reglas del juego dependen de dos enteros positivos $k,n$, los cuales son conocidos para ambos jugadores.

En este post voy a tratar de ilustrar, a través de un problema de geometría, la tesis de que la competencia experta en el problem solving requiere de una combinación de técnicas y conocimiento conceptual (de competencias conceptuales pero también procedimentales). 

Un problema no trivial de geometría

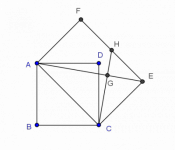
Tomando como base la diagonal $AC$ de un cuadrado $ABCD$, se construye un rectángulo $ACEF$ de altura el lado del cuadrado y con $D$ dentro de él.

 

Si $H$ es el punto medio de $EF$ y $G$ es la intersección de $AE$ con $CH$, demostrar que

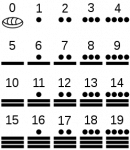
Los sistemas de numeración son símbolos y reglas para denotar cantidades  Muchas civilizaciones inventaron los suyos, por ejemplo, los romanos usaron la notación I, II, III, IV, .. etcétera.

En nuestros tiempos, el sistema de numeración que usamos cotidianamente se llama sistema de numeración posicional en base 10 (o simplemente sistema decimal).  Es decimal pues se usan diez símbolos (a saber  0, 1, 2, 3, 4, 5, 6, 7, 8, 9) y depende de la posición pues no es lo mismo 12 (uno dos) que 21 (dos uno).