Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Perpendiculares
Para un triángulo ABC, toma los puntos M y N en las extensiones de AB y CB, respectivamente de tal manera que M y N estén más cerca de B que de A y C, y que AM=CN=s donde s denota el semiperímetro. Sea K el punto diametralmente opuesto a B e I el incentro del triángulo ABC.
Midas en México... y con padrinos
Un empresario tiene que distribuir todas sus ganancias de los siguientes tres meses entre tres padrinos (después de eso queda liberado de los favores recibidos en forma de contratos).
Equilátero inscrito en equilátero
Inscribir un triángulo equilátero en un triángulo equilátero ABC, de tal manera que cada lado del inscrito sea perpendicular a un lado del triángulo ABC. (Describir el procedimiento de construcción.)
Problema 6G, Ciudades 2009
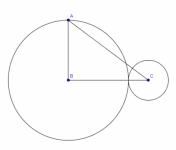
En la figura el segmento BC une los centros de los círculos tangentes, AB es perpendicular a BC,BC=8 , y AC=10. Calcular el área de cada círculo.
¿Incírculo o excírculo?
Sean D en AB y E en AC, los extremos de un segmento tangente al incírculo del triángulo ABC. Si los lados AB,BC,CA miden, respectivamente, c,a,b, expresar el perímetro del triángulo ADE en términos de a,b,c.
Medio rombo y un 30-60-90
Un rombo de lado 2m tiene un ángulo de 30∘. ¿Cuánto vale su área?
Método sui generis --de pesar al bebé
El papá quiere saber cuánto pesa su hijo recién nacido.
Busca divisores o paga lo que debes... al álgebra
Sean p y q números primos con p2 menor que q. Encontrar todos los enteros positivos n tales que al sumar p2q a su cuadrado el resultado es un cuadrado.
Inradio y cateto
Expresar el radio r del incírculo de un triángulo rectángulo isósceles en términos del cateto c.

Bellezas maduras (quirúrgicamente alteradas)
Roxi, Sara y Tess, ahora ya en su madurez, decidieron acudir a una clínica de cirugía cosmética con el fin de permanecer socialmente aceptables.
Exponente primo
Sean n un entero positivo, demostrar que si 2n−1 es un número primo, entoces n también es primo.
Área de un equilátero
Sea ABC un triangulo equilátero y R el radio de la circunferencia que lo circunscribe, demuestre que el area del triangulo es igual a: 3R2√3/4
El cuerudo no anda en burra
Un cierto día, al amanecer, el cuerudo tamaulipeco salió de Jaumave --en su cuaco retinto--hacia Tula.
Dígitos invertidos
Considere los números 84 y 36. Si sus dígitos se invierten tenemos los números 48 y 63. Pues sucede que el producto de cada uno de esos pares de números es 3024.
Área de un triángulo de lados desconocidos
Calcular el área y el perímetro de un triángulo si se sabe que las longitudes de sus lados satisfacen la ecuación x3−12x2+47x=60
Ecuación cuadrática y rectángulo
Calcular el área y el perímetro de un rectángulo si se sabe que las longitudes de sus lados satisfacen la ecuación cuadrática x2−10x+21=0.
Chicas Barbie
Krysta, Marcia y Nona tienen una vida adolescente común: salen a fiestas, van de compras, se preocupan por estar a la moda y coleccionan Barbies (más que una muñeca, en su opin
El "maistro" más marrulla del ejido
Abel, Bocho y Casiano, tres "maistros" especialistas en construcción de bardas de adobón, ganaron un contrato para construir una.
Un chico fresa
Blaine, un chico fresa de la ciudad, se fue a "macalear" (de compras a McAllen) el fin de semana. Se compró una cachucha, una playera y un par de zapatos tenis.
Alturas de un isósceles
En un triángulo acutángulo ABC, las alturas de B y C respecto a las bases CA y AB, respectivamente, se intersectan en el punto S. Sean M en AB y N en CA los pies de esas alturas. Demostrar que AB=CA si y sólo si el ángulo MSB mide el doble que el ángulo CBN.
