Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Partición de un conjunto
Encontrar todos los enteros positivos n para los cuales el conjunto A={n,n+1,n+2,n+3,n+4,n+5} puede particionarse en dos subconjuntos con el mismo producto de sus miembros (el producto de los números en uno de los subconjuntos es igual al producto de los números en el otro).
Residuo de un factorial (módulo un primo)
Encontrar el residuo que deja 50(50!) al dividirlo entre 53.
Inverso (mod 151) de una potencia de 2
Encontrar un número entero positivo que al multiplicarlo por 2145 y al resultado restarle 1, se obtenga un múltiplo de 151.
Expresable como combinación lineal
Decidir (con justificación) cuál de los tres números 2007,2008,2009 podría ser expresado como una combinación lineal entera de 453 y 408, es decir, en la forma 453x+408y, con x,y enteros.
Encontrar un residuo
Encontrar el residuo que deja 20092008 al dividirlo entre 9
El polo de la recta que pasa por el vértice y el punto de tangencia.
Sea ABC un triángulo y sean D, E y F los puntos donde la circunferencia circunscrita es tangente al lado BC, CA y AB. Llamemos D′ el punto donde la recta EF corta a la recta AB. Demuestra que:
a) D′ es el conjugado armónico de D con respecto al segmento AB.
b) Que la recta AD es la polar de D′ respecto al incírculo.
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
Clasificación de primos que dividen a un cuadrado más uno
Demuestra que si p es un primo impar que divide a n2+1 para algún n, entonces p debe ser de la forma 4k+1, es decir, p≡1 (mód 4).
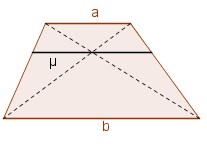
Media armónica de las bases de un trapecio.
Considere μ un segmento paralelo a las bases a y b de un trapecio, de tal manera que μ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que μ es la media armónica de a y b, es decir:
No es un cuadrado perfecto
Demostrar que si y es un entero, 187y−1 no es un cuadrado perfecto.
División anular
Sean a,b,c tres números enteros positivos tales que a divide a b2, b divide a c2 y c divide a a2. Demostrar que abc divide a a7+b7+c7.
Tres círculos congruentes
Tres círculos C1,C2,C3 del mismo radio se intersectan no tangencialmente en un punto P. Sean A,B los centros de C1,C2, respectivamente; y C,D los puntos de intersección de C1,C2, respectivamente, con C3. (C,D son ambos diferentes de P.) Demostrar que ABCD es un paralelogramo.
Interrupción de la filosofía --en Tijuana
Alejandra (de 37 abriles) fue apañada por un retén de la PGR en Tijuana, el día último de abril, apenas cruzó la aduana procedente de San Diego. Le incautaron 30000 US Dollars, producto de la recaudación por venta de coca en USA.
Una factorización notable (en la IMO 69)
Demuestre que existen infinitos m enteros positivos tales que n4+m es un número compuesto para cualquier n entero positivo.
Una factorización notable
Encontrar todos los enteros n tales que n4+4 es primo.
Cíclico en tres circunferencias tangentes
Considere C1, C2 y C3 tres circunferencia que por pares son tangentes externas. Llamemos P y Q los puntos de tangencia de C1 con C2 y C3 respectivamente.
Problema de coolinealidad
Sean C1,C2,C3 tres circunferencias tangentes exteriores dos a dos. Definamos los siguientes puntos; R=C1∩C2 S=C1∩C3 y T=C2∩C3 , sean X,Y los puntos sobre C2,C3 de modo que XY sea la tangente comun y esta no pase por C1. Sea J la interseccion de la tangente a C1,C2 por R y a la tangente comun a C1,C3 por S.
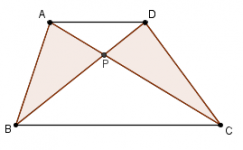
Áreas iguales en un trapecio
Demuestra que para cualquier trapecio ABCD, las áreas de las triángulos sombreados son iguales.
Sumas
Considere las sumas
S=4⋅5−5⋅6+…−2009⋅2010
T=3⋅6−4⋅7+…−2008⋅2011
Calcular el valor de S−T
Producto de diagonales en un polígono regular
Sea A1,A2,…,An los n vértices de un polígono regular con circunferencia circuncrita de radio R, Demuestra que:
