Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Juego de las 3 cartas
Tres jugadores, A,B,C, utilizan tres cartas para jugar. Es cada una de ellas está escrito un número entero positivo y todos son diferentes, digamos p,q,r en orden creciente.
Factores de 39
Si m,n son enteros positivos que cumplen la ecuación mn+mn+1+mn+2=39 encuentra sus valores (todos los posibles).
Teorema de Napoleón (interior)
Si en un triángulo ABC se construyen triángulos equiláteros interiores sobre sus lados, entonces los centros X,Y,Z de dichos triángulos equiláteros determinan un triángulo equilátero XYZ, conocido como triángulo de Napoleón interior. (Demostrarlo.)
Teorema de Napoleón (exterior)
Si en un triángulo ABC se construyen triángulos equiláteros exteriores sobre sus lados, entonces los centros X,Y,Z de dichos triángulos equiláteros determinan un triángulo equilátero XYZ, conocido como triángulo de Napoleón exterior. (Demostrarlo.)
Ladrones de la tercera edad
"El Carrizos" y "el Mayel", dos ladrones de la tercera edad, han robado un collar circular con 2m cuentas de oro y 2n cuentas de plata, dispuestas en un orden desconocido.
Dividir un segmento...
Dividir un segmento AC en la razón 3/2 (en razón de 3 a 2), internamente por un punto B y externamente por un punto G.
Congruentes, por tanto...
En la figura, los triángulos ABC y DEF son congruentes, con BC=EF. ¿Cuánto mide el ángulo EGC?
Ida y vuelta
Una persona camina de A a B a 4 km/h y de regreso de B a A camina a 6 km/h. Si tarda 45 minutos en la caminata de ida y vuelta ¿cuál es la distancia entre A y B?
Demostrar isósceles
En el triángulo ABC, las alturas CM y BN se cortan en el punto S. Con los datos que se muestran en la figura, concluye que el triángulo es isósceles.
Quita y pon canicas.
El siguiente juego de canicas involucra un sólo jugador. Se ponen muchas canicas en una caja.
Problema desargueano (parte 1)
Si en un triángulo ABC se toman los puntos P en BC, Q en CA yR en AB, de tal manera que las rectas QR,RP,PQ cortan a los lados BC,CA,AB en los puntos P′,Q′,R′, res
P1 OMM 2004 - Problema 1
Encuentra todos los números primos p,q,r con p<q <r , que cumplan
con 25pq+r=2004 y que pqr+1 sea un cuadrado perfecto
Ternas Pitagóricas (parte 3)
Demostrar que en cualquier terna pitagórica primitiva a2+b2=c2, exactamente dos de los números a,b,c son impares. (Primitiva significa sin divisores en común.)
Ternas Pitagóricas (parte 2)
Demostrar que en cualquier terna pitagórica a2+b2=c2, al menos uno de los números a, b, c es divisible entre 5.
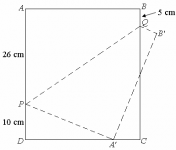
Geometría con origami
Una hoja de papel en forma rectangular ABCD se dobla a lo largo de la línea PQ de manera que el vértice A quede en el lugar del punto A′ y el vértice B en el lugar del punto B′. Al medir los segmentos AP,BQ,DP, se tiene que miden 26cm,5cm y 10cm, respectivamente.
¿Cuál es el área del la hoja de papel?
Problema 6, ONMAS 5 (modificado)
En un rectángulo de base 10 y altura 8, se ha inscrito un paralelogramo de tal manera que en las esquinas del rectángulo se forman triángulos de catetos 4 y 7 y 3 y 4. Encuentra la distancia entre los lados opuestos del paralelogramo inscrito en el rectángulo.
Problema 6 OMM 2003
Dado un entero n un cambio sensato consiste en sustituir n por 2n+1 ó 3n+2. Dos enteros positivos a y b se llaman compatibles si existe un entero que se puede obtener haciendo uno o más cambios sensatos, tanto a partir de a, como a partir de b. Encuentra todos los enteros positivos compatibles con 2003 menores que 2003.
Problema 4 OMM 2003
Sea ABCD un trapecio con AB paralelo a DC. Se toman puntos P y Q sobre AB y CD respectivamente, tales que APPB=DQQC. Sea M la intersección de AQ con DP y sea N la intersección de PC con QB. Pruebe que la longitud de MN depende sólo de las longitudes de AB y DC y calcula su valor.
Ciencias blandas (Soft science)
Tres licenciados en ciencias blandas han tenido que entrar al mercado laboral con sus habilidades preuniversitarias. Con la siguiente información decide en qué trabaja cada uno.
Triángulos de igual área
Demostrar que un cuadrilátero es paralelogramo si y sólo si cada una de sus diagonales lo divide en dos triángulos de igual área.
