Problemas
También puedes compartirnos alguno de tus problemas favoritos:
P5. IMO 2014 - Monedas fraccionarias
Para cada entero positivo n, el Banco de Ciudad del Cabo produce monedas de valor 1n. Dada una colección finita de tales monedas (no necesariamente de distintos valores) cuyo valor total no supera 99+12, demostrar que es posible separar esta colección en 100 o menos montones, de modo que el valor total de cada montón sea como máximo 1.
P4. IMO 2014 - Concurrencia de dos rectas y una circunferencia
Los puntos P y Q están en el lado BC del triángulo acutángulo ABC de modo que ∠PAB=∠BCA y ∠CAQ=∠ABC. Los puntos M y N están en las rectas AP y AQ, respectivamente, de modo que P es el punto medio de AM, y Q es el punto medio de AN. Demostrar que las rectas BM y CN se cortan en la circunferencia circunscrita del triángulo ABC
P3. IMO 2014 - Demuestra que es tangente
En el cuadrilátero convexo ABCD, se tiene ∠ABC=∠CDA=90∘. La perpendicular a BD desde A corta a BD en el punto H. Los puntos S y T están en los lados AB y AD, respectivamente, y son tales que H está dentro del triángulo SCT y
∠CHS−∠CSB=90∘,∠THC−∠DTC=90∘
Demostrar que la recta BD es tangente a la circunferencia circunscrita del triángulo TSH.
P2. IMO 2014 - Configuraciones pacíficas en un tablero
Sea n≥2 un entero. Consideremos un tablero de tamaño n×n formado por n2 cuadrados unitarios. Una configuración de n fichas en este tablero se dice que es pacífica si en cada fila y en cada columna hay exactamente una ficha. Halle el mayor entero positivo k tal que, para cada configuración pacífica de n fichas, existe un cuadrado de tamaño k×k sin fichas en sus k2 cuadrados unitarios.
P1. IMO 2014 - Sucesión Inifinita
Sea a0<a1<a2<⋯ una sucesión infinita de números enteros positivos. Demostrar que existe un único entero n≥1 tal que an<a0+a1+⋯+ann≤an+1
Números divertidos
Un entero positivo n es divertido si para todo divisor positivo d de n, d+2 es un número primo. Encuentre todos los npumeros divertidos que tengan la mayor cantidad posible de divisores.
Equiláteros sobre un segmento
Se marcan los puntos A, B, C, D sobre una recta, en ese orden, con AB y CD mayores que BC. Se construyen triángulos equiláteros APB, BCQ y CDR, con P, Q y R del mismo lado respecto a AD. Si el ángulo PQR mide 120 grados, pruebe que
1AB+1CD=1BC
1,5,13,25...
Con cuadrados de lado 1 se forma en cada etapa una figura en forma de escalera siguiendo el patron del dibujo
Por ejemplo, la primera etapa utiliza un cuadrado, la segunda utiliza 5. Determine la última etapa para la cual la figura correspondiente utiliza menos de 2014 cuadrados.

Todo es cuestión de álgebra
Sean a,b,c y d números todos distintos entre sí, tales que
ab+bc+cd+da=4 y ac=bd
Determine el máximo valor de posible de
ac+bd+ca+db
Así o más congruentes
Sea un trapecio ABCD de bases AB y CD , inscrito en una circunferencia de radio O. Sea P la intersección de las rectas AD y BC . Una circunferencia por O y P corta a los segmentos BC y AD en puntos interiores F y G respectivamente. Muestre que BF=DG .
Números "tico"
Un entero positivo se denomina tico si es el producto de tres números primos diferentes que suman 74. Verifique que 2014 es tico. ¿Cuál será el próximo año tico? ¿Cuál será el último año tico de la historia?
Inferencias con diofantina y clases residuales
r,r+p,r+2p primos , r=?
3.N. Encontrar todos los números primos que pueden escribirse como la diferenciade dos primos y como la suma de dos primos. (Nota: el 1 no es primo.)
Un problema guiado --de geometría
2.G. Sean ABC un triángulo isósceles con AB=AC, y P en AB y Q en AC puntostales que AP=CQ. Sea O la intersección de las mediatrices de PQ y AC.
a) Demostrar que APO y CQO son triángulos congruentes.
b) Demostrar que APOQ es un cuadrilátero cíclico.
c) Demostrar que AO es bisectriz del ángulo BAC.
(Nota: Para el inciso b puedes usar el resultado del a (sin demostración); para el cpuedes usar los resultados de a y b.)
¿Cuál fórmula? ¡Genera la lista!
1.C. ¿Cuántos números del 10 al 99 son tales que sus dígitos están en orden decreciente? Nota: 31 cumple pero no el 44 ni el 56.
Coeficientes y raíces en tres cuadráticas
2.6. Considere las ecuaciones cuadráticas
x2−b1x+c1=0x2−b2x+c2=0x2−b3x+c3=0
con b1.b2,b3,c1,c2,c3 números reales diferentes.
¿Es posible que los números b1,b2,b3,c1,c2,c3 sean las raíces de las ecuaciones cuadráticas en algún orden?
Configuración con acutángulo isósceles
2.5. Sea ABC un triángulo acutángulo isósceles con AC=BC. M y N son los puntos medios de AC y BC, respectivamente. La altura desde A corta a la prolongación de MN en X y la altura desde B corta a la prolongación de MN en Y. Z es la intersección de AY con BX. Además, sucede que los triángulos ABC y XYZ son semejantes. Determina la razón ACAB.
Tabla con números sin 3 o 7
2.4. Se tiene una tabla con siete columnas A,B,C,D,E,F,G y se coloca en ella los números naturales que no contienen al 3 o al 7 en su desarrollo decimal. Se empieza en la casilla C1, como se muestra. ¿En cuál columna y renglón queda el 2014?

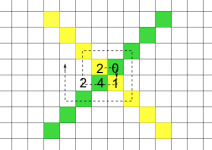
Espiral con el 2014 en cuadrícula
2.3. Sobre una cuadrícula se coloca 2014 veces el número 2014 (un dígito en cada casilla) siguiendo una espiral como se muestra en la figura. Sea M la suma de los números sobre las casillas verdes y N la suma de los números sobre las casillas amarillas. Calcula la diferencia entre M y N.
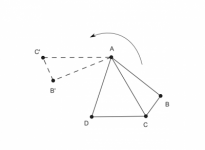
Ángulo postgiro
2.2. Sea ABCD un cuadrilátero que cumple: AB=AD,AC=BC+CD y los ángulos ABC y CDA suman 180 grados. El triángulo ABC se gira con centro en A formando el triángulo AB'C', como se muestra en la figura, hasta que el punto B' coincida con D, formándose el triángulo ADC'. Encuentra la medida del ángulo ACC'.