Problemas

En un cuadrado $ABCD$ de lado $60$. $E,F,G$ y $H$ son puntos medios de $AB,BC;CD$ y $DA$, respectivamente. Encuentra el área del hexágono $IJKLMN$.

Muestra que el número $5n+3$ no es un cuadrado perfecto, con n entero positivo y que si $2n+1$ y $3n+1$ son ambos cuadrados, entonces $5n+3$ no es primo.

Sea $p_1 , p_2 , p_3 \dots$   la sucesión de números primos ordenados de menor a mayor. Si $n \geq 2$, demuestra que $p_n + p_{n+1}$ se puede expresar como el producto de al menos tres enteros mayores que 1 (no necesariamente distintos). 

Muestra que para todo entero positivo n, primo relativo con 10 existen infinidad de múltiplos de n cuyos dígitos son solo unos. 

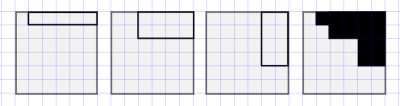
Sean $n$ un entero positivo y $k$ un entero entre $1$ y $n$. Se tiene un tablero de $n \times n$ color blanco. Se hace el siguiente proceso. Se dibujan $k$ rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos $k$ rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de $k$ rectángulos?

En una circunferencia se marcan 60 puntos, de los cuales 30 se colorean de rojo, 20 de azul y 10 de verde. La circunferencia queda así dividida en 60 arcos y a cada uno de ellos se les asigna un número de acuerdo a la siguiente regla:

--1 si une un punto rojo con uno verde
--2 si une un punto rojo con uno azul
--3 si une un punto azul con uno verde
--0 si une dos puntos del mismo color

¿Cuál es la mayor suma posible de los números asignados a los arcos? (Justifica tu respuesta.)

Para un entero positivo n denotamos con S(n) la suma de los dígitos y con U(n) el dígito de las unidades. Determinar todos los enteros positivos n con la propiedad de que n=S(n)+U(n)²  (Nota: Para n=324, S(n)=9 y U(n)=4.)