Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Ejercicio con baricentro y circuncentro
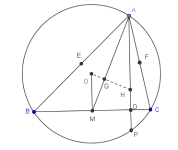
En la figura se muestra un triángulo $ABC$ y su circuncírculo. El segmento que va desde el circuncentro $O$ (concurrencia de mediatrices) al gravicentro $G$ (concurrencia de medianas) se ha prolongado hasta cortar a la altura $AD$ en $H$.
Demostrar:
- (a) Los triángulos $OMG$ y $HAG$ son semejantes
- (b) El segmento $GH$ mide el doble que el $OG$
- (c) En $H$ concurren las tres alturas
Ejercicio con ortocentro
En la figura, $H$ es la intersección de las alturas, y la altura $AD$ del triángulo $ABC$ se ha prolongado hasta cortar el circuncírculo en $P$.
Demostrar:
- (a) El triángulo $HBC$ es isósceles
- (b) La recta $BC$ es mediatriz de $HP$
- (c) Los puntos $H$ y $P$ son simétricos respecto al lado $BC$
Ortocentro, reflexión axial, circuncírculo
Demostrar que, en cualquier triángulo, el punto simétrico del ortocentro respecto a un lado es un punto del circuncírculo.
Divisibilidad entre el producto de tres primos (P6)
Sean $p,q,r$ números primos positivos distintos. Muestra que si $pqr$ divide a $$(pq)^r+(qr)^p+(rp)^q-1$$ entonces $(pqr)^3$ divide a $$3((pq)^r+(qr)^p+(rp)^q-1)$$
Circunferencia por ortocentro y dos vértices de un acutángulo (P5)
Cuadrícula n por 4 (P4)
Sea $n$ un entero positivo. En una cuadrícula $ n\times 4 $, cada renglón es igual a
| 2 | 0 | 1 | 0 |
Un cambio es tomar tres casillas
- consecutivas en el mismo renglón y
- con dígitos distintos escritos en ellas
y cambiar los tres dígitos de estas casillas de la siguiente manera
0 → 1, 1 → 2, 2→0
Dos circunferencias tangentes exteriormente (P3)
Sean $ C_1 $ y $ C_2 $ dos circunferencias tangentes exteriormente en un punto $ A $. Se traza una recta tangente a $ C_1 $ en $ B $ y secante a $ C_2 $ en $ C $ y $ D $; luego se prolonga el segmento $ AB $ hasta intersecar a $ C_2 $ en un punto $ E $. Sea $ F $ el punto medio del arco $ CD $ sobre $ C_2 $ que no contiene a $ E $ y sea $ H $ la intersección de $ BF $ con $ C_2 $. Muestra que $ CD,AF $ y $ EH $ son concurrentes.
Lectura de una tabla
La tabla de la figura muestra las frecuencias del número de puntos que los concursantes de la 24 Olimpiada Mexicana de Matemáticas obtuvieron en cada uno de los 6 problemas del examen nacional.
Cambios de estado de focos en un tablero (P2)
En cada casilla de un tablero $ n\times n $hay un foco. Inicialmente todos los focos están apagados. En un paso, se permite cambiar el estado de todos los focos en una fila o de todos los focos en una columna (los focos prendidos se apagan y los focos apagados se prenden). Muestra que si después de cierta cantidad de pasos hay uno o más focos prendidos entonces en ese momento hay al menos n focos prendidos.
Ternas que cumplen una ecuación (P1)
Encuentra todas las ternas de números naturales $ (a,b,c) $ que cumplan la ecuación $ abc=a+b+c+1 $.
Caracterización de alturas de un acutángulo
En el triángulo acutángulo $ABC$, los puntos $D,E,F$, ubicados respectivamente en los lados $BC,CA,AB$, son tales que $$CD/CE=CA/CB$$ $$AE/AF=AB/AC$$ $$BF/BD=BC/BA$$ Demostrar que $AD,BE,CF$ son alturas.
Huevos en la canasta
Cuántos huevos hay en la canasta si
División feminista
Un cubo perfecto
Un cierto número (entero positivo) multiplicado por 360 resulta en un cubo perfecto. Encontrarlo.
Rectángulo, lados, perímetro
Los lados de un rectángulo tienen longitudes enteras, una de ellas es 8 unidades menos que otra, y la suma de tres de ellas es 55. Encontrar el perímetro.
Suma algebraica
La suma de 4020 números enteros consecutivos es 2010. Encontrarlos.
Abuelo, nietos y domingo
El abuelo repartió 500 pesos entre sus 18 nietos de manera que cada niña recibió 2 pesos menos que cada niño. ¿Cuánto recibió cada quien en el reparto?
La amistad es una relación simétrica
En un grupo de personas, cada dos de ellas tiene exactamente un amigo en común en el grupo. Prueba que hay una persona que es amiga de todas las demás personas en el grupo. (Nota: la amistad es mutua, es decir, si X es amigo de Y, entonces Y es amigo de X.)
Incentro y bisectrices
En el triángulo $ABC$, el ángulo $BAC$ mide 60 grados. La bisectriz del ángulo $ABC$ corta al lado $AC$ en $X$ y la bisectriz del ángulo $BCA$ corta al lado $AB$ en $Y$. Demuestra que si $I$ es el incentro del triángulo $ABC$, entonces $IX=IY$
Fracción con mínimo denominador
De todas las fracciones $\frac{x}{y}$ que cumplen $$\frac{41}{2010}<\frac{x}{y}<\frac{1}{49}$$ encuentra la que tenga menor denominador.