Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Ejercicio con ortocentro
En la figura, H es la intersección de las alturas, y la altura AD del triángulo ABC se ha prolongado hasta cortar el circuncírculo en P.
Demostrar:
- (a) El triángulo HBC es isósceles
- (b) La recta BC es mediatriz de HP
- (c) Los puntos H y P son simétricos respecto al lado BC
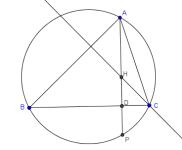
Ortocentro, reflexión axial, circuncírculo
Demostrar que, en cualquier triángulo, el punto simétrico del ortocentro respecto a un lado es un punto del circuncírculo.
Divisibilidad entre el producto de tres primos (P6)
Sean p,q,r números primos positivos distintos. Muestra que si pqr divide a (pq)r+(qr)p+(rp)q−1 entonces (pqr)3 divide a 3((pq)r+(qr)p+(rp)q−1)
Circunferencia por ortocentro y dos vértices de un acutángulo (P5)
Cuadrícula n por 4 (P4)
Sea n un entero positivo. En una cuadrícula n×4, cada renglón es igual a
| 2 | 0 | 1 | 0 |
Un cambio es tomar tres casillas
- consecutivas en el mismo renglón y
- con dígitos distintos escritos en ellas
y cambiar los tres dígitos de estas casillas de la siguiente manera
0 → 1, 1 → 2, 2→0
Dos circunferencias tangentes exteriormente (P3)
Sean C1 y C2 dos circunferencias tangentes exteriormente en un punto A. Se traza una recta tangente a C1 en B y secante a C2 en C y D; luego se prolonga el segmento AB hasta intersecar a C2 en un punto E. Sea F el punto medio del arco CD sobre C2 que no contiene a E y sea H la intersección de BF con C2. Muestra que CD,AF y EH son concurrentes.
Lectura de una tabla
La tabla de la figura muestra las frecuencias del número de puntos que los concursantes de la 24 Olimpiada Mexicana de Matemáticas obtuvieron en cada uno de los 6 problemas del examen nacional.
Cambios de estado de focos en un tablero (P2)
En cada casilla de un tablero n×nhay un foco. Inicialmente todos los focos están apagados. En un paso, se permite cambiar el estado de todos los focos en una fila o de todos los focos en una columna (los focos prendidos se apagan y los focos apagados se prenden). Muestra que si después de cierta cantidad de pasos hay uno o más focos prendidos entonces en ese momento hay al menos n focos prendidos.
Ternas que cumplen una ecuación (P1)
Encuentra todas las ternas de números naturales (a,b,c) que cumplan la ecuación abc=a+b+c+1.
Caracterización de alturas de un acutángulo
En el triángulo acutángulo ABC, los puntos D,E,F, ubicados respectivamente en los lados BC,CA,AB, son tales que CD/CE=CA/CB AE/AF=AB/AC BF/BD=BC/BA Demostrar que AD,BE,CF son alturas.
Huevos en la canasta
Cuántos huevos hay en la canasta si
División feminista
Un cubo perfecto
Un cierto número (entero positivo) multiplicado por 360 resulta en un cubo perfecto. Encontrarlo.
Rectángulo, lados, perímetro
Los lados de un rectángulo tienen longitudes enteras, una de ellas es 8 unidades menos que otra, y la suma de tres de ellas es 55. Encontrar el perímetro.
Suma algebraica
La suma de 4020 números enteros consecutivos es 2010. Encontrarlos.
Abuelo, nietos y domingo
El abuelo repartió 500 pesos entre sus 18 nietos de manera que cada niña recibió 2 pesos menos que cada niño. ¿Cuánto recibió cada quien en el reparto?
La amistad es una relación simétrica
En un grupo de personas, cada dos de ellas tiene exactamente un amigo en común en el grupo. Prueba que hay una persona que es amiga de todas las demás personas en el grupo. (Nota: la amistad es mutua, es decir, si X es amigo de Y, entonces Y es amigo de X.)
Incentro y bisectrices
En el triángulo ABC, el ángulo BAC mide 60 grados. La bisectriz del ángulo ABC corta al lado AC en X y la bisectriz del ángulo BCA corta al lado AB en Y. Demuestra que si I es el incentro del triángulo ABC, entonces IX=IY
Fracción con mínimo denominador
De todas las fracciones xy que cumplen 412010<xy<149 encuentra la que tenga menor denominador.
Seccionado recursivo
Sofía tiene 5 pedazos de papel en una mesa. Toma algunos de los pedazos, corta cada uno en 5 pedacitos y los vuelve a poner en la mesa. Ella repite este procedimiento varias veces hasta que se cansa. ¿Podría Sofía llegar a tener 2010 pedazos al final en la mesa?
