Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Cambios de estado en cuadrícula 6X6 --con luciérnagas
En cada cuadrado de una cuadrícula de 6×6 hay una luciérnaga apagada o encendida. Una movida es escoger tres cuadrados consecutivos, ya sean los tres verticales o los tres horizontales, y cambiar de estado a las tres luciérnagas que se encuentran en dichos cuadrados. (Cambiar de estado a una luciérnaga significa que si está apagada se enciende y si está encendida se apaga.) Muestra que si inicialmente hay una luciérnaga encendida y las demás apagadas, entonces no es posible hacer una serie de movidas tales que al final todas las luciérnagas estén apagadas.
Composición de la función "suma de sus dígitos"
Para un entero positivo n se definen n1 como la suma de los dígitos de n, n2 como la suma de los dígitos de n1, y n3 como la suma de los dígitos de n2.
Por ejemplo para n=199, n1=1991=19,n2=1992=10 y n3=1993=1.
Encuentra todas las parejas de enteros positivos (m,n) tales que:m+n=2007 m3+n3=20073
Desigualdad homogenea
Sean a,b,c números reales positivos que satisfacen a+b+c=1.
Muestra que: √a+bc+√b+ca+√c+ab≤2.
Lugar geométrico equiangular
Dado un triángulo equilátero ABC, encuentra todos los puntos P del plano que cumplan ∠APB=∠BPC.
Diez consecutivos son divisores --pero no 11
Encuentra todos los enteros positivos N con la siguiente propiedad: entre todos los divisores positivos de N, hay 10 números consecutivos, pero no 11.
La arista es el MCD de sus vértices
En los vértices de un cubo están escritos 8 enteros positivos distintos, uno
en cada vértice. Y en cada una de las aristas está escrito el máximo común
divisor de los números que están en los 2 vértices que la forman. Sean A la suma de los números escritos en las aristas y V la suma de los números escritos en los vértices.
- (a) Muestra que 23A≤V.
- (b) ¿Es posible que A=V?
Juego de caballeros
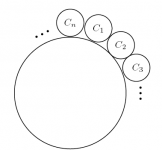
Los caballeros C1,C2,…,Cn, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con C1, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Caballos en el tablero
Considera un tablero de ajedrez. Los números del 1 al 64 se escriben en las casillas del tablero como en la figura:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
Expresado como suma de potencias --de sus primeros dos divisores
Sean 1=d1<d2<d3⋯<dk=n los divisores del entero positivo n. Encuentra todos los números n tales que n=d22+d33.
P6 OMM 2006. Problema con números surtidos
Sea n la suma de los dígitos de un entero positivo A. Decimos que A es “surtido” si cada uno de los enteros 1,2,…,n es suma de dígitos de A
- Demuestra que si 1,2,…,8 son sumas de dígitos de un entero A entonces A es surtido.
- Si 1,2,…,7 son sumas de dígitos de un entero A, ¿es A necesariamente surtido?
Nota: El número 117 no es surtido pues sólo 1=1,2=1+1,7=7,8=1+7,9=1+1+7 se pueden escribir como suma de dígitos de 117.
P5 OMM 2006. Altura de triángulo pedal
Sean ABC un triángulo acutángulo y, AD,BE y CF sus alturas. La circunferencia con diámetro AD corta a los lados AB y AC en M y N, respectivamente. Sean P y Q los puntos de intersección de AD con EF y MN, respectivamente. Demuestra que Q es el punto medio de PD.
P3 OMM 2006. Números 1..2n en cuadrícula 2Xn
Sea n un número entero mayor que 1. ¿De cuántas formas se pueden acomodar todos los números 1,2,…,2n en las casillas de una cuadrícula de 2×n, uno en cada casilla, de manera que cualesquiera dos números consecutivos se encuentren en casillas que comparten un lado de la cuadrícula?
P2 OMM 2006. Semejantes si y sólo si ángulo de 60
Sea ABC un triángulo rectángulo con ángulo recto en A, tal que AB<AC. Sea M el punto medio de BC y D la intersección de AC con la perpendicular a BC que pasa por M. Sea E la intersección de la paralela a AC que pasa por M con la perpendicular a BD que pasa por B. Demuestra que los triángulos AEM y MCA son semejantes si y sólo si ∠ABC=60°.
P1 OMM 2006. Los parientes de un número son sus múltiplos
Sea ab un número de dos dígitos. Un entero positivo n es “pariente” de ab si:
- El dígito de las unidades de n también es b.
- Los otros dígitos de n son distintos de cero y suman a.
Por ejemplo, los parientes de 31 son 31, 121, 211 y 1111. Encuentra todos los números de dos dígitos que dividen a todos sus parientes .
P6 OMM 2005. Un punto en la paralela a la bisectriz
Sea ABC un triángulo y AD la bisectriz del ángulo ∠BAC, con D sobre BC. Sea E un punto sobre el segmento BC tal que BD=EC. Por E traza la recta l paralela a AD y considera un punto P sobre l y dentro del triángulo. Sea G el punto donde la recta BP corta al lado AC y sea F el punto donde la recta CP corta al lado AB. Muestra que BF=CG)
P4 OMM 2005. Eliminar (ternas aritméticas) reordenando
Decimos que una lista de números a1,a2,…,am contiene una terna aritmética ai,aj,ak, si i<j<k y 2aj=ai+ak. Por ejemplo, 8,1,5,2,7 tiene una terna aritmética (8,5 y 2) pero 8,1,2,5,7 no. Sea n un entero positivo. Muestra que los números 1,2,…,n se pueden reordenar en una lista que no contenga ternas aritméticas.
P5 OMM 2005. Con cualquiera de las restantes se completa
Sea N un entero mayor que 1. En cierta baraja de N3 cartas, cada carta está pintada de uno de N colores distintos, tiene dibujada una de N posibles figuras y tiene escrito un número entero del 1 al N (no hay dos cartas idénticas). Una colección de cartas de la baraja se llama completa si tiene cartas de todos los colores, o si entre sus cartas aparecen todas la figuras o todos los números. ¿Cuántas colecciones no completas tienen la propiedad de que, al añadir cualquier otra carta de la baraja, ya se vuelven completas?
P3 OMM 2005. Infinidad de enteros en sucesión de fracciones
Determina todas las parejas (a,b) de enteros distintos de cero para las cuales es posible encontrar un entero positivo x primo relativo con b y un entero cualquiera y, tales que en la siguiente lista hay una infinidad de números enteros:
a+xyb,a+xy2b2,a+xy3b3,…,a+xynbn,…
P2 OMM 2005. Matrices n-balanceadas
Dadas varias cuadrículas del mismo tamaño con números escritos en sus casillas, su suma se efectúa casilla por casilla. Por ejemplo:
Dado un entero positivo N, diremos que una cuadrícula es N-balanceada si tiene números enteros escritos en sus casillas y si la diferencia entre los números escritos en cualesquiera dos casillas que comparten un lado es menor o igual que N.

P1 OMM 2005. Circuncírculo en circuncírculo
Sea O el centro de la circunferencia circunscrita al triángulo ABC, y sea P un punto cualquiera sobre el segmento BC (P≠B y P≠C). Supón que la circunferencia circunscrita al triángulo BPO corta al segmento AB en R (R≠A y R≠B) y que la circunferencia circunscrita al triángulo COP corta al segmento CA en el punto Q (Q≠C y Q≠A).
- (i) Considera el triángulo PQR; muestra que es semejante al triángulo ABC y que su ortocentro es O.
- (ii) Muestra que las circunferencias circunscritas a los triángulos BPO,COP y PQR son todas del mismo tamaño.
