Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Construir un cuadrado inscrito a otro
Sean ABCD un cuadrado y M un punto en el interior de éste. Construir con regla y compás un cuadrado PQRS con sus vértices sobre los lados de ABCD y que M esté sobre alguno de los lados de PQRS.
Incentro y circuncírculo
Dado un triángulo ABC, sea I su incentro y L el punto donde la linea AI intersecta al circuncirculo . Demuestra que AL/LI=(AB+AC)/BC.
Un problema de lógica
Cuatro miembros de la banda XYZ comían un día juntos en una fonda chiquita. Eran dos mujeres, La Buchona y La Gitana, y dos hombres, El Talibán y El Cochiloco. Cada uno tenía un oficio diferente: Burrero, Gatillero, Guardaespaldas y Oreja. (La mesa era cuadrada y para cuatro.) Con los siguientes datos encontrar el oficio de cada quien.

Un problema de edades
Hace 10 años Jesús tenía la misma edad que Lourdes tiene ahora. Dentro de 7 años Madonna tendrá dos veces la edad de Jesús, aunque actualmente tiene 3 años más que cuatro veces la edad de Lourdes.

Contar clasificando
¿Cuántos triángulos hay en la figura?
IX Olimpiada Norestense de Matemáticas (Problema 3)
El incírculo del triángulo △ABC es tangente al lado AB en el punto P y al lado BC en el punto Q. El círculo que pasa por los puntos A,P,Q corta por segunda vez a la recta BC en M y el círculo que pasa por los puntos C,P,Q corta por segunda vez a la recta AB en el punto N.
Eliminación con dos operaciones
En cada cuadrado de un tablero rectangular hay un entero positivo. Se pueden modificar los números del tablero usando alguno de los siguientes movimientos.
--Multiplicar por 2 cada número de un renglón.
--Restar 1 a cada número de una columna.
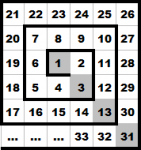
Números en espiral
Considera la sucesión {1,3,13,31,…} que se obtiene al seguir en diagonal el siguiente arreglo de números en espiral.
Encuentra el número en la posición 100 de esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 6)
Alrededor de una circunferencia se marcan 6000 puntos y cada uno se colorea con uno de 10 colores dados, de manera tal que entre cualesquiera 100 puntos consecutivos siempre figuran los 10 colores. Hallar el menor valor k con la siguiente propiedad: Para toda coloración de este tipo existen k puntos consecutivos entre los cuales figuran los 10 colores.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 5)
La sucesión an está definida por
a1=1,a2k=1+ak y a2k+1=1a2k, para todo entero k≥1.
Demostrar que todo número racional positivo aparece exactamente una vez en esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea ABC un triángulo con AB≠AC. Sean I el incentro de ABC y P el otro punto de intersección de la bisectriz exterior del ángulo A con el circuncírculo de ABC. La recta PI intersecta por segunda vez al circuncírculo de ABC en el punto J. Demostrar que los circuncírculos de los triángulos JIB y JIC son tangentes a IC y a IB, respectivamente.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean C1 y C2 dos circunferencias de centros O1 y O2, con el mismo radio, que se cortan en A y en B. Sea P un punto sobre el arco AB de C2 que está dentro de C1. La recta AP corta a C1 en C, la recta CB corta a C2 en D y la bisectriz del ∠CAD intersecta a C1 en E y a C2 en L. Sea F el punto simétrico a D con respecto al punto medio de PE. Demostrar que existe un punto X que satisface ∠XFL=∠XDC=30∘ y CX=O1O2.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 2)
Para cada entero positivo n se define an=n+m, donde m es el mayor entero tal que 22m≤n2n. Determinar qué enteros positivos no aparecen en la sucesión an.
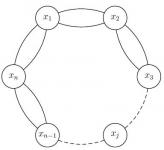
XXIV Olimpiada Iberoamericana de Matemáticas (problema 1)
Sea n un natural mayor que 2. Supongamos que n islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura:
Olimpiada Iberoamericana (el 4 de 2008)
Demuestra que no existen enteros positivos x,y tales que x2008+2008!=21y
Olimpiada Iberoamericana (el 4 de 2004)
Determinar todas las parejas (a,b), donde a,b son enteros positivos de dos dígitos cada uno, tales que 100a+b y 201a+b son cuadrados perfectos de cuatro dígitos.
Olimpiada Iberoamericana (el 5 de 1985)
A cada número natural n se le asigna un entero no negativo f(n) de tal manera que se satisfacen las siguientes condiciones:
- (i) f(rs)=f(r)+f(s)
- (ii) f(n)=0, si el dígito de las unidades de n es 3
- (iii) f(10)=0
Hallar f(1985)
Olimpiada Iberoamericana (el 1 de 1999)
Halla todos los enteros positivos que son menores que 1000 y cumplen con la siguiente condición: el cubo de la suma de sus dígitos es igual al cuadrado de dicho entero.
Olimpiada Iberoamericana (el 4 de 1987)
Se define la sucesión pn de la siguiente manera: p1=2 y, para n≥2, pn es el mayor divisor primo de p1p2…pn−1+1. Demostrar que pn es diferente de 5.
¿Cómo lograr más con menos?
Del conjunto de números {1,2,...,99,100} se eligen 50. Si la suma de los números elegidos es 2900, calcular el número mínimo de números pares entre los 50 elegidos.
