Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Cambio de dígitos
Sean a y b enteros positivos de 8 dígitos cada uno, tales que al quitar cualquier dígito de a (pero solo uno) y colocar el correspondiente en posición con b, se cumple que el número formado es divisible entre 7 (en cualquiera de los 8 posibles cambios). Demuestra que b es divisible entre 7.
Equilátero seccionado (3G, take_home_1)
Sea ABC un triángulo equilátero y A’, B’ , C’, puntos sobre los lados BC, CA y AB, respectivamente, tales que AC′/C′B=BA′/A′C=CB′/B′A=2 Las intersecciones de los segmentos AA’, BB’ y CC’ determinan un triángulo interior, digamos, DEF.
Una propiedad trivial de la potencia de un punto
Sean dados tres puntos distintos O, P, Q en el plano. Demostrar que OP=OQ si y sólo si P y Q tienen la misma potencia respecto a un círculo cualquiera con centro en O.
IMO 2009, Problema 3
Sea s1,s2,s3,… una sucesión estrictamente creciente de enteros positivos tal que las
subsucesiones
ss1,ss2,ss3,… y ss1+1,ss2+1,ss3+1,…
son ambas progresiones aritméticas. Demostrar que la sucesión s1,s2,s3,... es también una progresión
Problema 5(N)
El alumno menos aventajado del salón canceló el 6 en 16/64 y obtuvo 1/4 --la respuesta correcta. Encontrar todos los pares de números de dos cifras ab, bc tales que ab/bc=a/c --con a,b,c dígitos diferentes. (Es decir, todos los casos en que este alumno podría acertar con su método al simplificar quebrados de dos cifras.)
IMO 2009 Problema 1
Sea n un entero positivo y sean a1,a2,...,ak(k≥2) enteros distintos del conjunto 1,...,n, tales que n divide a ai(ai+1−1), para i=1,...,k−1. Demostrar que n no divide a ak(a1−1).
IMO 2009 Problema 2
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.
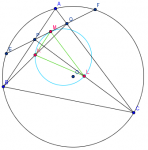
IMO 2009 Problema 4
En un triángulo ABC, donde AB=AC, los bisectrices internas de ∠A y ∠B cortan a los lados BC y AC en D y E, respectivamente. Sea I el incentro del triángulo ADC. Supongamos que ∠IEB=45. Encontrar todos los valores posibles de ∠A.

Probar isósceles
En una semicircuferenica de diámetro AB se elige un punto D y se baja una perpendicular al diámetro AB cortándolo en C. En el espacio descrito por DC, CB y el arco BD se inscribe un círculo tangente a CD en L, a BC en J y al arco BD en K. Demostrar que AD=AJ.
Encontrar el término n de una sucesión
Considere la sucesión a1=1 y, para n mayor que 1, an=1+2an−1. Encontrar una fórmula para el término n-ésimo y demostrarla por inducción.
Potencia de un punto y circunferencias ortogonales
Sean dados una circunferencia c de radio r y centro O, y dos puntos M y M' tales que OM⋅OM′=r2 (i.e., inversos uno del otro respecto a c). Demostrar que cualquier circunferencia c' que pase por M y M' es ortogonal a c.
Condición necesaria y suficiente para cíclicos
Sea PQRS un cuadrilátero tal que sus lados opuestos PR y QS se cortan en un punto T. Demostrar que PQRS es cuadrilátero cíclico si y sólo si TR⋅TP=TS⋅TQ.
El lugar geométrico de la reflexión de un punto
Sean P un punto en el interior de una circunferencia C y M un punto sobre C. Definamos N el punto sobre C tal que el ángulo ∡MPN=90∘ (en sentido contrario de las manecillas del reloj). Llamemos P′ el punto que resulta de reflejar P con respecto a MN.
Construcción de una circunferencia ortogonal
Sea dada una circunferencia c. Demostrar que el siguiente procedimiento produce una circunferencia ortogonal a c con centro en un punto P fuera de c.
1) Trazamos las tangentes a c desde P ubicando los puntos de tangencia T y T′.
2) Trazamos la circunferencia con centro en P y radio PT. Esta es la circunferencia ortogonal pedida.
Caracterización del eje radical
Demostrar que el eje radical de dos circunferencias es el lugar geométrico de los puntos que cumplen la propiedad de que el producto de la suma por la diferencia de sus distancias a los centros es una constante.
Valor de la potencia de un punto
Demostrar que la potencia de un punto P respecto a la circunferencia c con centro en O y radio r es PO2−r2
Construcción del inverso
Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el inverso P' de P con respecto a la circunferencia c.
1) Trazar la recta OP.
2) Trazar una de las tangentes desde P a c, y llamar T al punto de tangencia.
Trazar una tangente a una circunferencia
Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el punto de tangencia T de la tangente que pasa por P.
1) Trazar el segmento OP.
2) Trazar la circunferencia de diámetro OP y llamar T a uno de los puntos de intersección con c.
Altura de un triángulo rectángulo
Sea AP la altura de A respecto a la hipotenusa BC del triángulo rectángulo ABC. Demostrar que se cumplen las proporciones PB/BA=BA/BC y BP/PA=PA/PC.
Cuerda común y línea de centros
La línea de centros (recta que pasa por los centros) de dos círculos que se intersectan es mediatriz de su cuerda común.
