Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Palabras en un alfabeto
¿Cuántos números de 5 dígitos tienen todos sus dígitos de la misma paridad y ninguno de sus dígitos es el cero? Nota: se dice que dos números son de la misma paridad si ambos son pares o ambos son impares.
Regiones 2009, problema 1
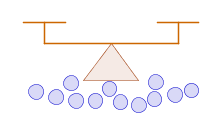
¿De cuántas formas se pueden colocar los números 0,1,2,3,4,5,6, uno en cada casilla del siguiente panal, sin que haya 2 múltiplos de 3 en casillas adyacentes (i.e., con un lado en común)?
El fácil del Regiones 2009
¿Cuántos números abcd de 4 dígitos distintos, múltiplos de 36 y menores que 4000 son tales que el producto de ab por cd es múltiplo de 7?
Diofantina condicionada
Encontrar todos las parejas de enteros positivos (x,y) que sean solución de la ecuación diofantina 20x+9y=2009, y que además sean cuadrados perfectos consecutivos. Nota: (x,y)=(100,1) y (x,y)=(1,221) son soluciones de la ecuación diofantina pero no cumplen la condición.
Propiedades del máximo común divisor
Demostrar las siguientes propiedades del máximo común divisor de dos números a y b. Nota: hay dos formas usuales de notación para el máximo común divisor, MCD(a,b) o simplemente (a,b).
Trivial --pero no para el novicio
Demostrar que n2−1 es múltiplo de 8 para cualquier n impar no negativo.
Diofantina en dos variables
Encontrar todas las parejas (x,y) de enteros que satisfacen la ecuación diofantina x3+y3=4(x2y+xy2)+1.
Lema de Euclides --instancia de uso
Encontrar todas las parejas (a,b) de enteros positivos para los cuales el producto (a4+1)(b2−1) es divisible entre 39 pero sus factores (a4+1) y (b2−1) no.
P1. OMM 1987. Suma de dos fracciones que dan entero
Consideremos dos fracciones reducidas ab y cd con b,d>0 . Si la suma de estas dos fracciones es un número entero entonces b=d.
Problema 1, ONMAS 2008
¿Cuántos divisores cuadrados perfectos tiene el número 20082008 ?
Problema 1, geometrense 2008
En un circunferencia hay 3n puntos que la dividen en 3n arcos. De estos arcos n miden 1, n miden 2 y el resto mide 3. Demuestra que existen dos de estos puntos diametralmente opuestos.
Diez cajas de billar y una báscula electrónica.
Tenemos 10 cajas con bolas de billar; cada caja pesa 10kg y contiene 10 bolas de billar (1kg cada una). Pero, una de las cajas salió defectuosa, aunque todas sus bolas pesan lo mismo, la caja completa pesa 9kg. Es decir, en una de las cajas, todas la bolas pesan 900 gramos.
Doce bolas y tres pesadas
Determinar, con el auxilio de una balanza y en sólo tres pesadas, una bola de entre doce, que pesa distinto a las demás. Además, determinar si la bola pesa más o menos que las otras.
Yoga de leche
Una yoga de 5 litros está llena de leche. Dos botellas vacías de 2 y 3 litros respectivamente están disponibles para transferir el líquido entre las botellas y la yoga de 5 litros. Exhibir un procedimiento para lograr 4 litros de leche en la yoga de 5 litros. Encontrar una sucesión de transferencias de leche de longitud 3.
Las cervezas de Bart Simpson
Bart Simpson cuenta, usando sus dedos de la mano derecha, las cervezas que se ha tomado su papá en la semana. Si cuenta empezando con el meñique y termina en el índice pulgar y vuelve a empezar con el meñique, y contó 777 ¿en qué dedo terminó la cuenta? (Nota: Bart solamente tiene 4 dedos. Además, hay que suponer que sabe contar hasta 777...) ¿En qué dedo terminaría si tuviese 5 dedos?

Fermat converso (en general, espurio)
Demostrar que si p,q son dos primos distintos para los cuales ap≡a(modq) y aq≡a(modp), entonces apq≡a(modpq). }
Demostrar, con este resultado, el siguiente contraejemplo para la conversa del pequeño teorema de Fermat: 2340≡1(mod341) --¡pero 341 es compuesto!
Una factorización no trivial
Factorizar las siguientes expresiones algebraicas:
x4+6x3+11x2+6x+1
x4+6x3+11x2+6x
Genera un problema de concurso, en vista de las dos factorizaciones.
Ángulos en el reloj
¿Cuál es el ángulo que forman las manecillas del reloj a las 9:30? (Argumento fiador requerido.)
Problema 6, XII Olimpiada Iberoamericana
Sea P={P1,P2,…,P1997} un conjunto de 1997 puntos en el interior de un círculo de radio 1, siendo P1 el centro del círculo. Para cada k=1,…,1997 sea xk la distancia de Pk al punto de P más próximo a Pk y distinto de Pk. Demostrar que:
x21+x22+⋯+x21997≤9
P3. OMM 1993
Dentro de un pentágono de área 1993 se encuentran 995 puntos. Considere estos puntos junto con los vértices del pentágono.
Muestre que, de todos los triángulos que se pueden formar con los 1000 puntos anteriores como vértices, hay al menos uno de área menor o igual que 1.
