XXII OMM 2008

En los vértices de un cubo están escritos 8 enteros positivos distintos, uno
en cada vértice. Y en cada una de las aristas está escrito el máximo común
divisor de los números que están en los 2 vértices que la forman. Sean $A$ la suma de los números escritos en las aristas y $V$ la suma de los números escritos en los vértices.

• (a) Muestra que $\frac{2}{3}A\leq V$.
• (b) ¿Es posible que $A = V$?

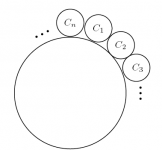
Los caballeros $C_1,C_2,\ldots,C_n$, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:

El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $C_1$, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.

Considera un tablero de ajedrez. Los números del 1 al 64 se escriben en las casillas del tablero como en la figura:

  1       2       3        4       5        6       7       8
  9     10     11     12     13     14     15     16
17     18     19     20     21     22     23     24

Sean $1=d_1 < d_2 < d_3 \cdots < d_k = n$ los divisores del entero positivo $n$. Encuentra todos los números $n$ tales que $n = d_2 ^ 2 + d_3^3$.

Las bisectrices internas de los ángulos A, B y C de un triángulo ABC concurren en I y cortan
al circuncírculo de ABC en L, M y N, respectivamente. La circunferencia de diámetro IL,
corta al lado BC, en D y E; la circunferencia de diámetro IM corta al lado CA en F y G;
la circunferencia de diámetro IN corta al lado AB en H y J. Muestra que D, E, F, G, H,
J están sobre una misma circunferencia.

Considera una circunferencia $\Gamma$, un punto A fuera de $\Gamma$ y las tangentes AB, AC a $\Gamma$ desde A, con B y C los puntos de tangencia. Sea P un punto sobre el segmento AB, distinto de A y de B. Considera el punto Q sobre el segmento AC tal que PQ es tangente a $\Gamma$, y a los puntos R y S que están sobre las rectas AB y AC, respectivamente, de manera que RS es paralela a PQ y tangente a $\Gamma$. Muestra que el producto de las áreas de los triángulos APQ y ARS no depende de la elección del punto P.

Muestra que el producto de las áreas de los triángulos APQ y ARS no depende de la elección del punto P.