Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Elemental,... pero sólo si sabes usar el PTF
Encontrar todos los primos q tales que 4+2q es múltiplo de 2q.
Progresión aritmética con un cuadrado
Demostrar que si una progresión aritmética de enteros positivos contiene un cuadrado perfecto entonces contiene infinitamente muchos cuadrados perfectos.
Los primos no se factorizan... excepto en la forma 1( p )
Encontrar todos los enteros positivos n tales que n20+n10+1 es un primo.
Otro de puros 1´s
Demostrar que todo primo impar n excepto el 5 divide a algun numero de la forma 111...11 (k digitos, todos unos).
P divide a una sumota
Sea p un número primo. Encontrar la condición que debe cumplir n para que 1+n+n2+....+np−2 es múltiplo de p.
Encontrar k...
Determina si existen infinitos enteros k, que cumplen que para cualquier primo p, el numero p2+k siempre es compuesto.
Por ejemplo si tomamos k=2, para p=2 dicho numero es compuesto pero para p=3 no lo es...
Semicírculo y la descomposición en dos sumandos de un segmento.
Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que BP=PQ+QC
División en casos
Encontrar todas las tripletas (p,q,r) de números primos tales que pq+pr es un cuadrado perfecto.
Criba modular
Encontrar todas las soluciones (x,y) en enteros positivos para la ecuación 7x−3⋅2y=1.
Múltiplo de 11 compuesto de unos
Sea p un un entero positivo. El número 11p está compuesto de m dígitos todos iguales a 1. Encontrar todos los valores de m para los cuales p es primo.
Áreas enteras de triángulos
El área del triángulo ABC es un entero. Sobre los lados BC y AC se eligen los puintos X y Y, respectivamente. Los segmentos AX y BY se cortan en un punto P dentro del triángulo ABC. El área de BPX es 1, la de APY es 2, y la de APB es un entero. Encontrar el área del triángulo ABC.
Biblioteca
En mi biblioteca hay 5 libros de álgebra, 6 de combinatoria, y 8 de geometría, y todos son diferentes.
a) ¿De cuántas formas puedo elegir dos?
b) ¿De cuántas formas puedo elegir dos del mismo tema?
c) ¿De cuántas formas puedo elegir dos pero que no sean del mismo tema?
Partir la baraja
Sea n un entero positivo. Una baraja de 2n cartas contiene exactamente dos cartas marcadas con cada uno de los enteros 1,2,…,n. Las cartas se ordenan en la forma 1,1,2,2,3,3,...,n,n. La baraja ya ordenada de esta manera se parte, y resulta que, en las dos partes, los dígitos en las cartas suman la misma cantidad.
Segmentos iguales y colinealidad
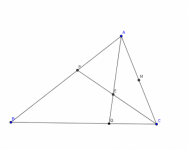
Sea ABC un triangulo, M el punto medio de CA, P el punto donde la bisectriz desde C intersecta a AB; E y Q son los puntos donde una ceviana desde A intersecta a la bisectriz y al lado BC, respectivamnete (Q no esta en la prolongacion de BC). Demuestra que los segmentos PQ y CQ son iguales, si y solo si B, E y M son colineales.
Los cuadernos del Chico Fresa
El Chico Fresa recién regresó de Italia y les trajo cuadernos a sus cuates. ¿De cuántas formas puede distribuir los 15 Moleskine entre 4 de sus amigos, bajo la condición de que a Baldo le toquen al menos 3, a Carlos al menos 2 y a Daniel al menos 1? (Nota: a Eulogio le puede tocar cualquier número --lo siento el chico fresa tiene sus preferidos.)
Cuadrilátero cícliclo dentro de un cuadrilátero circunscrito
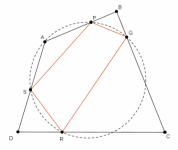
Sea ABCD un cuadrilátero para el cuál existen cuatro puntos P, Q, R y S sobre los lados AB, BC, CD y DA respectivamente y tales que PB=BQ, QC = CR, RD = DS y SA = AP. Demuestra que:
- a) El cuadrilátero ABCD es circunscrito
- b) El cuadrilátero PQRS es cíclico.
Problema 4 OIM 1997
Sea n un entero positivo. Consideremos la suma x1y1+x2y2+…+xnyn, donde los valores que pueden tomar las variables x1,x2,…,xn,y1,y2,…,yn son únicamente 0 y 1. Sea I(n) el número de 2n-adas (x1,x2,…,xn,y1,y2,…,yn) para las cuales el valor de la suma es un número impar y sea P(n) el número de 2n-adas (x1,x2,…,xn,y1,y2,…,yn) para las cuales la suma toma valor par. Probar que
P(n)I(n)=2n+12n−1
IMO 2009, Problema 5
Determinar todas las funciones f del conjunto de los enteros positivos en el conjunto de los enteros positivos tales que, para todos los enteros positivos a y b, existe un triángulo no degenerado cuyos lados miden
a,f(b) y f(b+f(a)−1)
(Un triángulo es no degenerado si sus vértices no están alineados).
P1. OMM 1988. Siete pelotas blancas y cinco negras
¿De cuántas formas se pueden acomodar en línea recta siete pelotas blancas y cinco negras, de tal manera que no estén dos pelotas negras juntas?
IMO4_2009_invertido
Sean ABC un triángulo isósceles rectángulo en A, J su incentro y AD, BE las bisectrices de los ángulos A y B, respectivamente. La altura AD es tangente al incírculo del triángulo ADC (con incentro en I) en P y al lado CA en Q. Demostrar que:
