Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Baldor debería saberlo...
El producto N de tres números enteros positivos es 6 veces la suma de tales números, y uno de los enteros es la suma de los otros dos. Calcular la suma de todos los valores posibles de N.
¿Trazo auxiliar? OK Pero... ¿cómo lo descubres?
En un triángulo isósceles AOB, rectángulo en O, se eligen los puntos P,Q,S en los lados OB,OA,AB, respectivamente, y un punto R interior al triángulo, de tal manera que el cuadrilátero PQRS sea un cuadrado. Si la razón de áreas entre el cuadrado y el triángulo es 2/5, calcular la razón OP/OQ.
Una propiedad de dos primos
Si p y q son primos, entonces pq−1+qp−1−1 es múltiplo de pq
Primos y menores
Sea p un primo y r un entero positivo. ¿Cuántos enteros positivos menores que pr son primos con pr?
Autoinversos respecto a un módulo
Sea p un primo, a un elemento de {1,2,3,...,p−1} y a tal que a2≡1(modp). Encontrar los posibles valores de a.
Sin Euler estaríamos perdidos
Encontrar las tres últimas cifras de 20099999 (argumento fiador requerido).
El PTF lo resuelve --si le piensas un poquito...
Encontrar todos los primos q tales que 4+2q es múltiplo de 2q.
Un corolario del PTF
Si p es un primo impar y a es primo con p, entonces ap−12≡±1(modp). (Por ejemplo, todo cuadrado perfecto primo con 5 termina en 1 o en 9 o en 4 o en 6.)
La clave está en los residuos
Encontrar todas las parejas (x,y) de dígitos, tales que el número 2x1y9 sea múltiplo de 101.
Elemental pero difícil
Encontrar todos los números enteros positivos de cuatro cifras de la forma n=abab (la primera y la tercera cifras son iguales, así como la segunda y la cuarta) y tales que el producto de sus cifras divide a n2.
Divisible entre la suma de sus cifras
Demostrar que en un conjunto de 18 números enteros positivos, consecutivos y menores o iguales a 2009, hay uno que es divisible entre la suma de sus cifras.
Factorizar y resolver
Encontrar todas las soluciones (x,y) en enteros positivos de la ecuación diofantina x3=19+y3
Una diofantina muy difícil
Resolver la ecuación diofantina siguiente para enteros no negativos x,y,z:
x2+y4+z6=21111
Inferencias de paridad
Sea n≥2 un entero. Los números x1,x2,…,xn son elementos del conjunto {−1,1} y cumplen la ecuación x1x2+x2x3+…+xnx1=0. Demostrar que n es múltiplo de 4.
Adictos al Xbox
Los adolescentes de una preselección olímpica de matemáticas tienen una actividad de entretenimiento favorita: 17 son adictos al Xbox (conjunto A1), 13 a las series americanas de TV (A2), 8 a la resolución de problemas de concurso (A3), y 6 no tienen actividad recreativa conocida.
Pudorosa (segunda parte)
Decidir --con prueba-- si la ecuación diofantina 123x+426y=8 tiene solución.
Una pudorosa propiedad del máximo común divisor
Si a,b son enteros y cumplen 7a−38b=−2 ¿qué se puede concluir sobre el máximo común divisor de a y b?
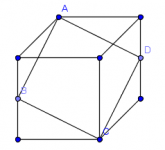
Cuadrilátero en un cubo
En un cubo de arista 6 los puntos medios B,D de dos aristas opuestas, y dos vértices opuestos A,C pero no en las aristas de los puntos medios B,D, forman un cuadrilátero ABCD. Encontrar el área de ese cuadrilátero.
¿Es múltiplo de 11? (Que lo diga Fermat.)
Decidir --con prueba-- si 6161+7171 es divisible entre 11.
ExSel2_Pr1: Inclusión y exclusión... pero basta con razonarlo
¿Cuántos números enteros positivos no mayores que 1000 no son ni cuadrados ni cubos?
