Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Longitud Mínima
Sea ABC un triángulo y P un punto que se mueve sobre la recta que contiene al lado BC. Consideremos M y N los pies de las perpendiculares trazadas desde P sobre los lado AB y AC respectivamente. Encuentra el punto P para el cual MN tiene longitud mínima.
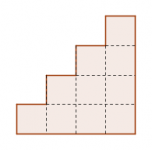
P4 OMM 2006. Zacatecas 2006: n-cubrimiento de una n-escalera
Como se sabe, en problemas de olimpiada, el enunciado puede tener una trampa de significado. El problema 4 del XX concurso nacional de la Olimpiada Mexicana de Matemáticas consiste de una pregunta “para qué enteros…”. La mayoría de los concursantes respondieron a la pregunta. Pero a la hora de las revisiones se supo que no bastaba con decir “estos son” sino que había que demostrar que no había otros. La solución necesitaba estar en el formato “los enteros n cumplen la condición si, y sólo si, son de la forma n = f(k)”. He aquí el enunciado del problema 4 del concurso nacional de 2006.
Un teorema sobre primos
Para todo primo p, si p2+2 es primo entonces p3+2 es también primo.
Ternas Pitagóricas
Demuestre que para cualquier terna pitagórica a2+b2=c2, alguno de los números a,b,c es divisible por tres.
Sucesión Aritmética y prueba de coprimalidad
Si ninguno de los números b,2b,...,(m−1)b es divisible entre m, entonces m y b son coprimos.
Un problema interesante de exponentes
Problema. Encontrar todos los enteros positivos a,b tales que ab=ba
Monterrey 97
Como se sabe, uno de los 6 problemas del concurso nacional de la Olimpiada Mexicana de Matemáticas es trivial –por lo menos para quienes han tenido un buen entrenamiento. He aquí el enunciado del primer problema del concurso nacional de 1997.
Encuentra todos los números primos positivos p tales que también sea un primo positivo.
XX Avanzados
Encuentra todas las parejas de números (a,b) tales que a−b es un número primo y el producto ab es un cuadrado perfecto.
Algoritmo Glotón y Criba
Construir un subconjunto B de A={1,2,…,40} tal que |B|=26 (el tamaño de B) y si b1 y b2 están en B entonces b1b2 no es cuadrado perfecto.
Longitud mínima - caso particular
Sean ABC un triángulo rectángulo en A, y P un punto móvil en la hipotenusa BC.
2n-agono
Demostrar que para cada n natural mayor que 1, cualquier 2n-ágono convexo tiene una diagonal que no es paralela a ningún lado.
Cinco Enteros
En cualquier conjunto de cinco enteros siempre hay tres cuya suma es múltiplo de 3.
Ecuaciones funcionales
Resolver las siguientes ecuaciones funcionales.
-
Encontrar p(x) de tal manera que p(x+1)=p(x)+2x+1.
-
Encontrar f(x) de tal manera que f(x+1)=x2−3x+2.
-
Lo mismo para f(x+1x)=(x2+1x2)+1/x
-
f(x+y)=f(x)+f(y)+f(x)f(y).
-
Para x>0, f(xy)=xf(y)+yf(x).
-
f(x+1)+f(x−1)=2x2−4x.
El problema 6 de la OMM 2005
Como se sabe, uno de los 6 problemas del concurso nacional de la Olimpiada Mexicana de Matemáticas es muy difícil –incluso para aquellos concursantes que han tenido un buen entrenamiento. He aquí el enunciado del problema 6 del concurso nacional de 2005.
Sea ABC un triángulo y AD la bisectriz del ángulo BAC, con D sobre BC. Sea E un punto sobre el segmento BC tal que BD=EC. Por E traza l la recta paralela a AD y considera un punto P sobre l y dentro del triángulo. Sea G el punto donde la recta BP corta al lado AC y sea F el punto donde la recta CP corta al lado AB. Muestra que BF=CG.
El Tesoro Pirata
En el mapa está un roble, un pino y un mezquite. Las instrucciones son: camina desde el mezquite hacia el pino, gira a la izquierda en ángulo recto, camina la misma distancia que hay del mezquite al pino, y clava ahí una estaca X; después regresa al mezquite, camina hacia el roble, gira a la derecha en ángulo recto, camina la misma distancia que hay entre el roble y el mezquite, y clava ahí una estaca Y. El tesoro está enterrado en el punto medio del segmento XY. ¿Qué hacer si el mezquite ha desaparecido?
El Viajero
Un viajero decide tomar un paseo en su propio automóvil, recorriendo un camino "circular" que pasa por n ciudades; es decir, sin importar en la ciudad que inicie, regresará a ésta después de pasar por las otras.
La distancia total del recorrido es de K kilómetros. Por otro lado, cada ciudad (digamos la ciudad i, con i entre 1 y n) tiene un máximo de gasolina que puede vender por usuario y con dicha gasolina se puede avanzar alguna cierta cantidad de kilómetros (Ki kilómetros para la ciudad i).
Supongamos que el total de gasolina que se puede obtener en las distintas ciudades es apenas suficiente para realizar todo el recorrido, es decir, K1+K2+...+Kn=K.
Fórmulas de Vieta
Encontrar todas las soluciones del siguiente sistema de tres ecuaciones en tres incógnitas.
Hagamos un trato (Let's make a deal –The Monty Hall Paradox)
Suponga que en un show de la televisión usted está participando y el animador le da a elegir tres puertas: lo que hay detrás de la elegida es suyo. Detrás de una de ellas está un auto nuevo, detrás de las otras dos una chiva. Imagine que usted elige una de las puertas, digamos la 1, y en ese momento (antes de abrirla) el conductor, quien sabe qué hay detras de cada puerta, abre una de las dos restantes, digamos la 3, y resulta que ahí hay una chiva. A continuación te pregunta “¿deseas cambiar tu elección (abrir la puerta 2)?”
¿Te conviene cambiar?
IMO 2004, problema 2
Encuentre todos los polinomios P(x) tales que
P(a−b)+P(b−c)+P(c−a)=2P(a+b+c)
para todo a,b,c reales que satisfacen que ab+bc+ca=0.
